|
|
|
|
Distortions in a non-uniform magnetic field. |
|
|
|
|
|
|
Last modified: 14:00 Wednesday 01-Aug-2001 |
The motion of charged particles under the influence of electric and magnetic fields, E and B, may be understood in terms of an equation of motion:
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(1)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(1)
where m and e are the mass and electric charge of the particle, u is its velocity vector, and K describes a frictional force proportional to u, which is caused by the interaction of the particle with gas.
The ratio m/K has the dimension of characteristic time, and we define†
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
†††††††††††(2)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
†††††††††††(2)
If t >> t the particle is moving with out any acceleration it
means that ![]() .
.
Using (2) the drift velocity vector can be determined by the linear equation
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
†††††††††††††(3)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
†††††††††††††(3)
We can define ![]() †etc.
†etc.
A different way of writing (1) is the following:
![]() ††††††††††††††††††††††††††††††††††††††††††† (4)
††††††††††††††††††††††††††††††††††††††††††† (4)
where ![]() †and
†and ![]() ,
,![]() denote the unit vectors in the directions of the fields.
denote the unit vectors in the directions of the fields.
And ![]() †we should never forget that
†we should never forget that ![]() change
sign depending from the charge of the particle.
change
sign depending from the charge of the particle.
We have special interest in the case where E nearly parallel to B. †
Letís just remind our self the definition of Cross Product.
Vector A is a cross product of vectors B and C where
![]() †and
†and ![]() †where
†where
![]() ;
;![]() ;
;![]() ;
;
In the case of E nearly parallel to B,
we can say that ![]() ,
,
![]() †where
†where ![]() .
.
Using (4) we can find ![]() .
.
![]() †††††
†††††
![]()
![]()
Mainly we are interested in relations between ![]() †and
†and ![]() .
.
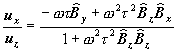 ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(5)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(5)
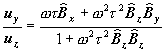 †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(6)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(6)
We can see that these relations arenít depending from the direction of the E field.
Letís make some approximation till the second order of approximation.
In that case:
![]() †† ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (7)
†† ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (7)
Using (7) the different way of writing (5) is the following:
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
So using those approximation we can re-write (5) and (6) in the following way:
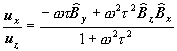 † ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††(8)†††††
† ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††(8)†††††
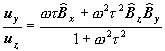
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(9)††††
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(9)††††
As we see these relations depend from the direction of the B field.
And the ![]() †where the charge of the particle can change
the sign of the
†where the charge of the particle can change
the sign of the ![]() .
.
We can easily rewrite those equations in the cylindrical coordinates:
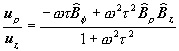 †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(8í)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(8í)
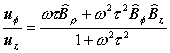 ††††††††† ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††(9í)
††††††††† ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††(9í)
Now letís see these equations in the case where![]() ,
,
![]() †where
†where ![]() .
.
Using (4) we can find three components of the velocity as we have done previously.
![]() †††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††††††††††††(10)
†††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††††††††††††(10)
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(11)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(11)
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (12)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (12)
Making the same approximation as in the previous case we have:
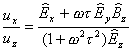 ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(13)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(13)
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(14)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(14)
The same equations in cylindrical coordinates are:
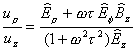 ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(13í)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
(13í)
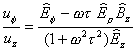 ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
†††††††††††††(14í)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††
†††††††††††††(14í)
So for both of this cases we can calculate the distortions.
![]()
So the master equations for calculating the distortions in a (slightly) non-uniform magnetic field are:
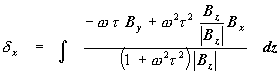 ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (15)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (15)
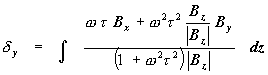 †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (16)†††††††
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (16)†††††††
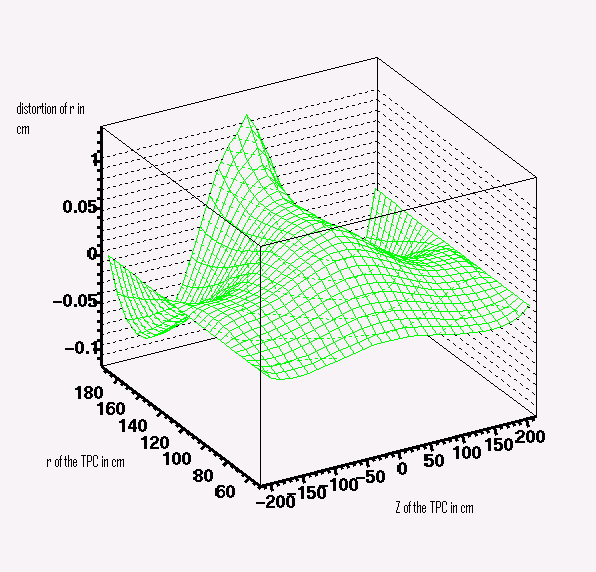
This image illustrates the distortion in TPC for non uniform magnetic field.
Where ![]() .
.
So these equations are the real equations that we use to calculate the distortions in the TPC.