Implications of signal sharing between rows:

A cluster of charge deposited in the TPC drift volume at (X,Y,Z), always yields a signal on more than one pad row, both due to the transverse diffusion that spreads the electrons across multiple anode wires, and to the finite width of the charge distribution induced on the pad plane by each wire. In estimating these effects, drift lines will be assumed to be parallel to Z for simplicity.

There are several implications of the signal correlations between rows:

• The particle's path length that contributes signal to the inner-subsector pad rows --- which are significantly separated from each other, but still share the signals from nearby anode wires over uninstrumented pad plane ("pseudo pad rows") --- is increased. This reduces the contribution of diffusion to the hit errors and improves the dE/dx resolution.

• For outer-subsector pad rows --- which are immediately adjacent to one another --- the available dE/dx information is increased only for the inner- and outer-most rows, but correlations between the signals on the rows will smooth, and broaden, the distribution of dE samples. This affects the best choice for a dE/dx algorithm (i.e., discarding the largest 30% of the dE samples no longer yields optimal results).

• Also for the outer subsector, the contribution of the crossing-angle and dip-angle effects to the X and Z errors of hits will be anti-correlated for adjacent pad rows. As a result, the errors for hits from tracks with moderate-to-large crossing angles tend to cancel, so that the hit should have more weight in the track fit than the 1-D residuals distributions would suggest.

• Conversely, the contribution of transverse and longitudinal diffusion to the X and Z errors of hits in adjacent pad rows will be positively correlated. Therefore, hits from tracks with small crossing angles should be given less weight in the track fit than the 1-D residuals distributions would suggest.

• In the outer subsector, signals from adjacent pad rows provide some Y information for tracks that travel along a pad row without crossing.

Transverse diffusion in P10:

The following approximate values for transverse diffusion in P10 were used in the simulations for this study:

Magnetic Field (Tesla)	Transverse Diffusion Constant (cm^0.5)	Max. Diffusion: Sigma after 210-cm Drift (cm)
0.00	0.0540	0.783
0.25	0.0355	0.514
0.50	0.0225	0.326

Diffusion can have effects somewhat beyond the range that the values in this table might seem to imply: hits in the STAR TPC will have a large dynamic range, and a hit with a large energy deposit will affect a hit with a small energy deposit at greater distance than for two with similar energy depositions. The table below shows the effect.

ADC Contribution of Cluster	Range: 3 ADC Count Effect (sigma)
20	1.95
40	2.28
200	2.90
1000	3.41

In general, the range of the effect is about 3 sigma, so we will use this as a rule of thumb to find the range of the effect at zero and maximum drift length from diffusion alone. Since the anode wires are spaced at 0.4 cm, we can also estimate the number of wires that have to be considered for an electron cluster.

Magnetic Field (Tesla)	"3-sigma" Diffusion Range, (cm)	Number of Anode Wires
0.00	0.00 - 2.35	1 - 6
0.25	0.00 - 1.54	1 - 4
0.50	0.00 - 0.98	1 - 3

To find the "3-sigma" range of the signal on the pad plane in centimeters, we must also include the width of the charge distribution induced by an anode wire (~0.161 cm for the inner subsector and ~0.323 cm for the outer subsector). We calculate the range of the effect for zero and maximum drift length. Note that, at maximum drift length and low B field, the range can exceed the pad-row pitch: to fully simulate effects due to the large dynamic range of signal, one may need two pseudo pad rows, rather than one, on either side of a real pad row.

Magnetic Field (Tesla)	"3-sigma" Range, Inner Subsector (cm)	"3-sigma" Range, Outer Subsector (cm)
0.00	0.48 - 2.40	0.97 - 2.54
0.25	0.48 - 1.62	0.97 - 1.82
0.50	0.48 - 1.09	0.97 - 1.38

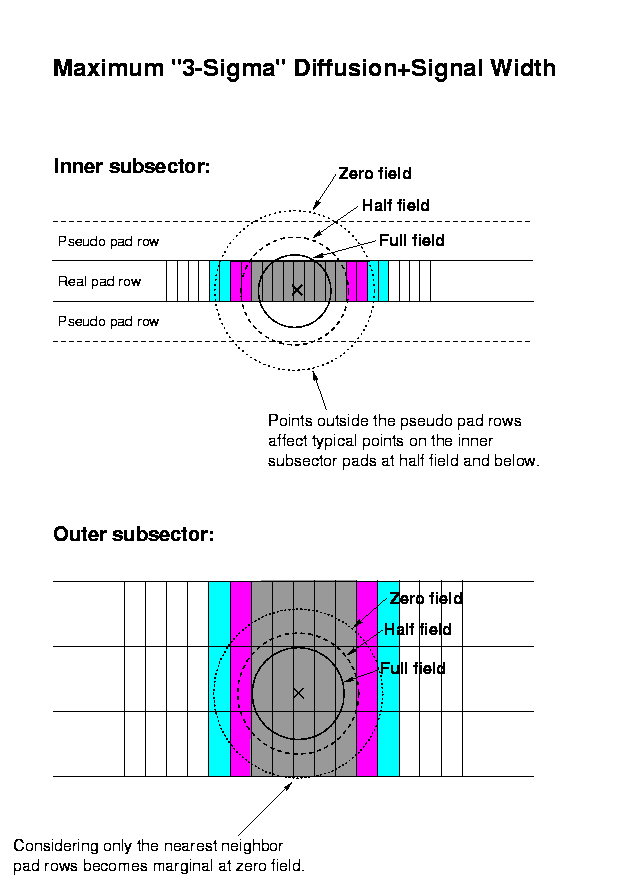
Fig. 1: Maximum "3-sigma" area that a typical pad location influences, and is influenced by,
due to transverse diffusion and the width of the charge distribution induced on the pad plane.
The grey, magenta and cyan-colored pads show the approximate range of the influence at
full, half and zero field, respectively, for the pads marked with X's.

Anode to pad row couplings:

The estimated anode-wire couplings are given as the fraction of a wire's signal induced on the pad row centered beneath Wire #0 --- the "reference" pad row --- relative to that induced on the pad plane as a whole. A wire induces a significant signal only on the pad row beneath it --- the "dominant" pad row --- and its nearest neighbors. Treating the coupling to any other row as identically zero is an excellent approximation. Wires are spaced on 0.4-cm centers, with symmetry around the pad row middle.

Inner subsector pads are pitched at 1.2 cm in Y and have 3 wires over each pad row. To preserve symmetry and unitarity, the coupling f(i) of each wire i to the reference pad row obeys the relations:

Sum f(i) = 3
f(i) = f(-i)
f(i) + f(i-3) + f(i+3) = 1

Outer subsector pads are pitched at 2.0 cm in Y and have 5 wires over each pad row. The coupling f(i) of each wire i to the reference pad row obeys the relations:

Sum f(i) = 5
f(i) = f(-i)
f(i) + f(i-5) + f(i+5) = 1

Calculated anode to pad row couplings:

Wire	Coupling (Inner)	Coupling (Outer)
0	0.9886	0.9749
+/- 1	0.8693	0.9372
+/- 2	0.1305	0.7271
+/- 3	0.0057	0.2722
+/- 4	0.0002	0.0602
+/- 5	0.0000	0.0125
+/- 6	0.0000	0.0026
+/- 7	0.0000	0.0005

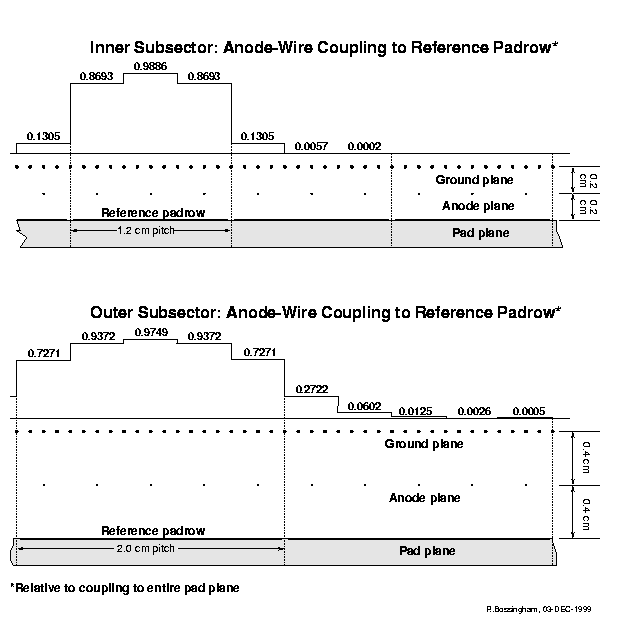
Fig. 2: Fraction of the signal from nearby anode wires induced on the reference pad row
(relative to that induced on the pad plane as a whole) for the STAR TPC.

Typical signal sharing onto pad rows:

For charge clusters having the same size and values of X and Y, the signal fraction induced on neighboring rows will be larger for longer drift distances and for lower magnetic fields (due to transverse diffusion). These dependencies are clearly visible in Figs. 3, 4 and 5 (for which the initial charge was distributed uniformly in Y across the reference pad row). The Z (drift-length) dependence is more pronounced for the inner subsector because of its smaller ratio of pad-row pitch (1.2-cm, rather than 2.0-cm) to transervse-diffusion width.

Note that, for the inner subsector, "nearest neighbors" refers to pseudo pad rows, not the real ones at considerable separation. Any meaningful simulations must include at least one set of pseudo pad rows bracketing each real row, but one can see from Fig. 5, that, for the inner subsector at low magnetic fields, a second pair is also needed (but not currently implemented in GSTAR).

Please increase the width of your browser window until the figures below are displayed side by side (for clarity):

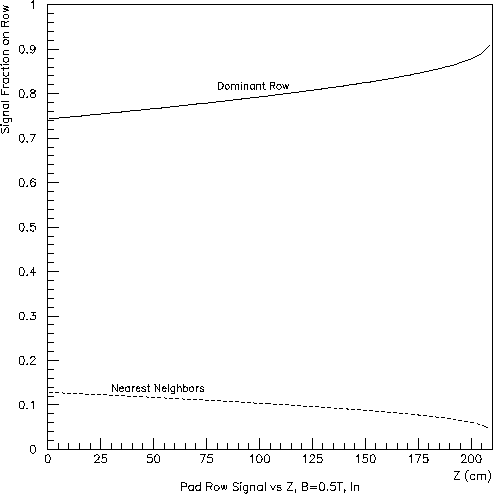
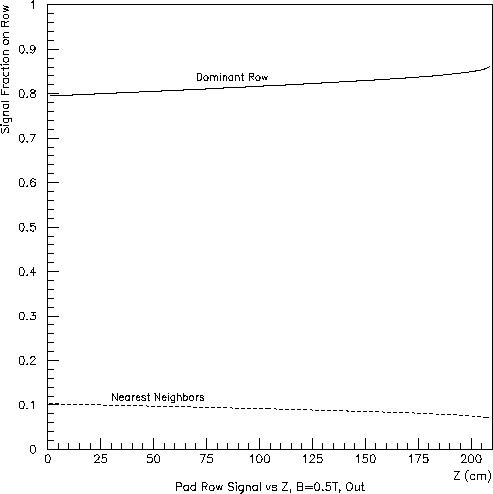
Fig. 3: Inner subsector (left) and outer subsector (right) at full field (B=0.5 T): signal fraction appearing in the dominant pad row and each nearest neighbor vs. Z.
The calculation assumed uniform charge deposition above the dominant pad row at each Z and a transverse diffusion constant of 0.0225 cm^0.5.

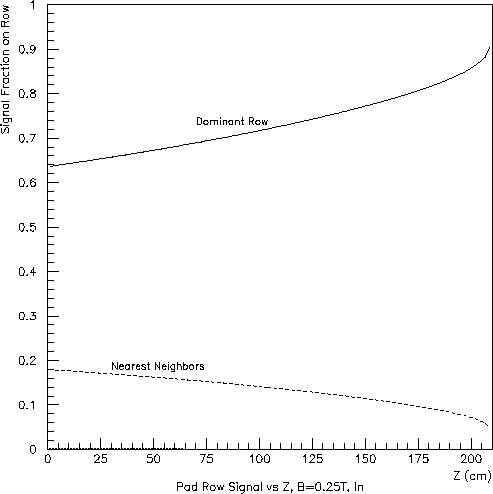
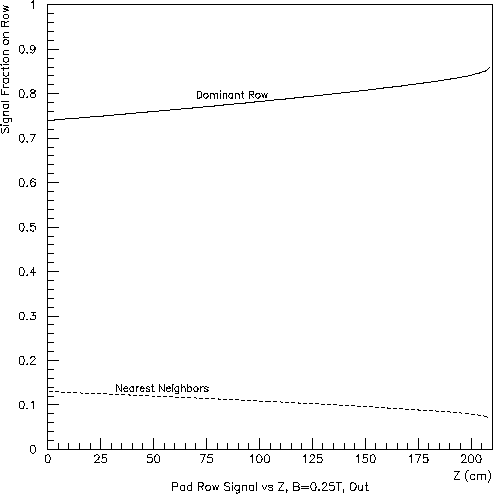
Fig. 4: Inner subsector (left) and outer subsector (right) at half field (B=0.25 T): signal fraction appearing in the dominant pad row and each nearest neighbor vs. Z.
The calculation assumed uniform charge deposition above the dominant pad row at each Z and a transverse diffusion constant of 0.0355 cm^0.5.

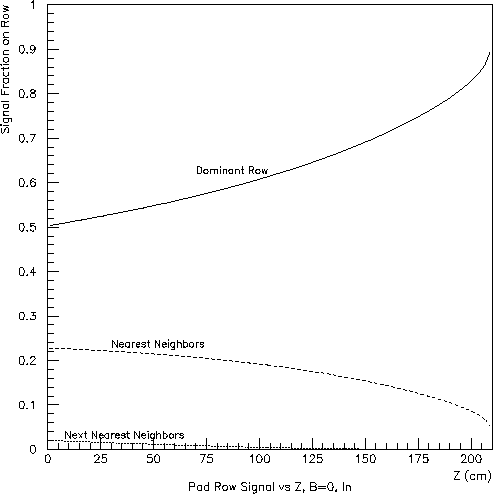
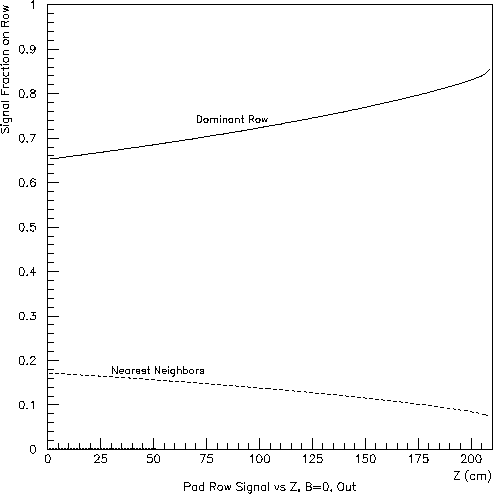
Fig. 5: Inner subsector (left) and outer subsector (right) at zero field: signal fraction appearing in the dominant pad row and each nearest neighbor vs. Z.
The calculation assumed uniform charge deposition above the dominant pad row at each Z and a transverse diffusion constant of 0.0540 cm^0.5.

Y Dependence of signal sharing onto pad rows:

Next, consider the Y-dependence of the "coupling" between hits in neighboring pad rows. The ratios of the signal on the nearest neighbor, to that on the dominant, pad row versus Y/(pad length) are shown in Figs. 6, 7 and 8. Here, Y=0 refers to the center of the dominant pad row. Clearly, the ratio will be 1.0 for Y/(pad length)=0.5, when the charge is half-way between two pad rows (or, for the inner subsector, between a real and pseudo pad row.

While no serious calculation has been done (to my knowledge), Figs. 6, 7 and 8 give some idea as to the Y resolution available for hits from tracks traveling along a pad row in the outer subsector. Recalling that the pads provide X information at a 20:1 signal:noise ratio, the Y resolution would probably be at the level of one-tenth pad length.

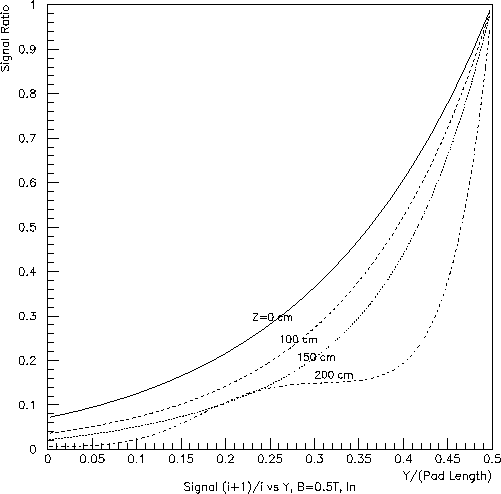
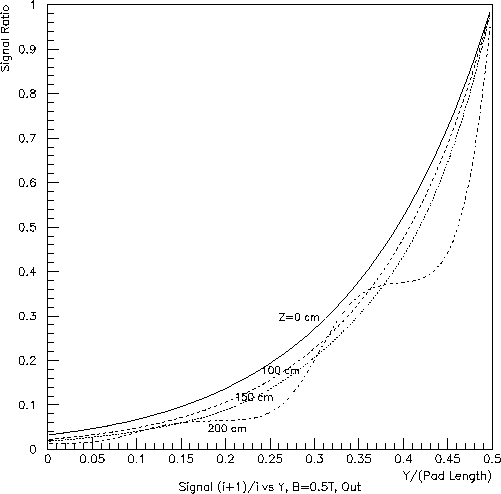
Fig. 6: Inner subsector (left) and outer subsector (right) at full field (B=0.5 T): ratio of the nearest-neighbor pad-row signal to the dominant pad-row signal vs. position
as a fraction of the pad length. The calculation assumed a transverse diffusion constant of 0.0225 cm^0.5.

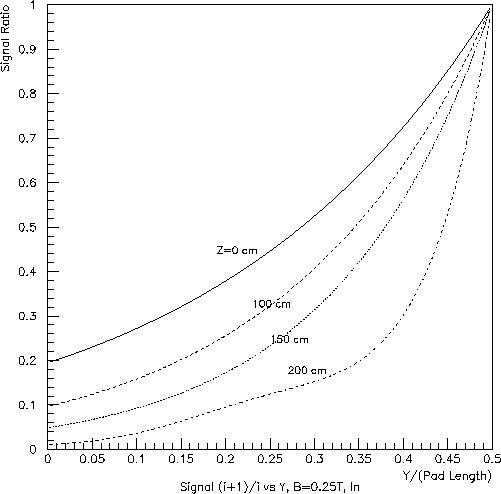
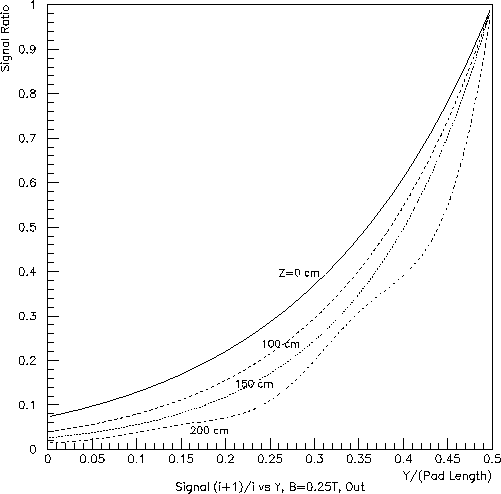
Fig. 7: Inner subsector (left) and outer subsector (right) at half field (B=0.25 T): ratio of the nearest-neighbor pad-row signal to the dominant pad-row signal vs. position
as a fraction of the pad length. The calculation assumed a transverse diffusion constant of 0.0355 cm^0.5.

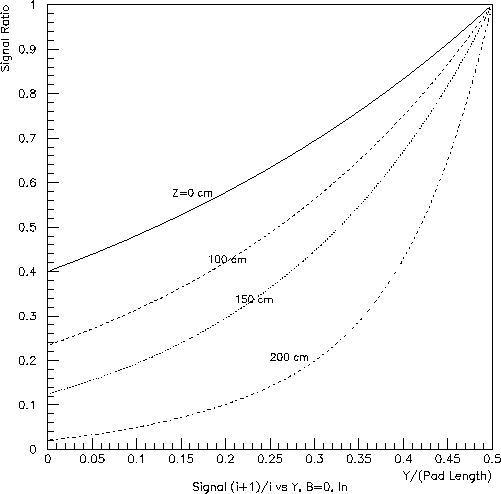
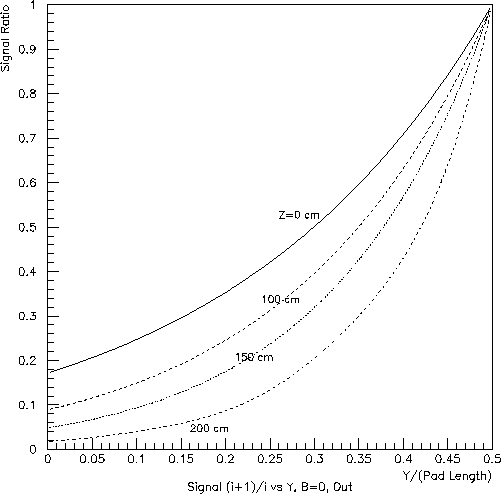
Fig. 8: Inner subsector (left) and outer subsector (right) at zero field: ratio of the nearest-neighbor pad-row signal to the dominant pad-row signal vs. position
as a fraction of the pad length. The calculation assumed a transverse diffusion constant of 0.0540 cm^0.5.