Next: Physics Programme for Data Up: Introduction Previous: Introduction Contents
CP is a symmetry that relates particles and antiparticles. If CP would be an exact symmetry than it would be hard to explain why our universe consist almost exclusively of matter and hardly any antimatter can be found.
Charge conjugation (C, particles are replaced by their antiparticles) and Parity (P, Space Inversion) are discrete operators. They are conserved symmetries in strong interactions but they are maximally violated in weak interactions. However, it was thought for some time that the combination of the two is conserved in weak interactions. But in 1964 a small CP violation was observed in the Kaon system.
The Standard Model offers the following explanation: the eigenstates of the
weak interaction of quarks do not coincide with the
mass eigenstates, the transition between the two bases is described by the
Cabbibo-Kobayashi-Maskawa (CKM) matrix ![]() :
:
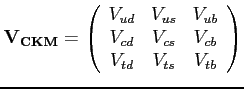
This matrix is unitary, so its parameters are bound by unitarity
relations. Four parameters of the matrix remain free. In the Wolfenstein [#!wolf!#]
parametrisation, the parameters are expanded in powers of the Cabbibo angle
![]() .
.
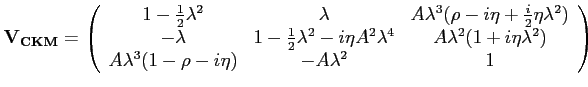
where is ![]() = sin
= sin![]() .
One of these parameters is complex (
.
One of these parameters is complex (![]() ) and it is the one that
is responsible for CP violation. The unitarity constraints can
be displayed as triangles in the complex plane where the sides are
products of the CKM matrix parameters. One of such triangles is shown
below:
) and it is the one that
is responsible for CP violation. The unitarity constraints can
be displayed as triangles in the complex plane where the sides are
products of the CKM matrix parameters. One of such triangles is shown
below:
In order to measure CP violation in the B system, ![]() or
or
![]() mesons have to be produced, their flavour tagged, and their decays
reconstructed. The design of HERA-B was optimized for the
measurement of the ``Golden Decay'':
mesons have to be produced, their flavour tagged, and their decays
reconstructed. The design of HERA-B was optimized for the
measurement of the ``Golden Decay'':
which through the asymmetry in the rates of the decays of ![]() and
and ![]() mesons to the same final state will give sin2
mesons to the same final state will give sin2![]() ,
one of the angles of the unitarity triangle, with very little
theoretical uncertainties:
,
one of the angles of the unitarity triangle, with very little
theoretical uncertainties:
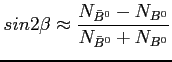
Other decays such as:
Yury Gorbunov 2010-10-21