MC Study Results

During comparison many efficiency studies were performed, the results obtained for the scenario one $J/\Psi \rightarrow \mu ^+\mu ^-$ event mixed with 2 superimposed inelastic events are summarized below in Table 4.2.

Table 4.2: Reconstruction efficiencies and clone/ghost rates obtained on simulated $J/\Psi \rightarrow \mu ^+\mu ^-$ events mixed with 2 superimposed inelastic events for CATS, RANGER and TEMA packages for realistic scenario.

		Efficiency (%)
Set	CATS	RANGER	TEMA
Ref. $J /\Psi$	97.4	93.6	90.8
Ref. Prim.	96.2	91.5	87.4
Ref. Tracks	92.3	84.6	82.7
All Tracks	55.6	40.	44.8
Extra	33.3	13.	21.7
Clone	2.1	2.5	0.8
Ghost	14.	17.2	17.1
MC tracks per event	59	42	47

On average, the CATS efficiency is 97% for reference tracks coming from the target region. The efficiencies for the other types of tracks are smaller, which can be attributed to their average momenta being smaller than those of primary and $J/\psi$ tracks.

The ghost rate is roughly 14%. It should be noted that the ghost rate at this level of reconstruction is uncritical because ghost tracks are very likely to be removed at the next steps, the magnet tracking or matching with VDS segments. The overall clone rate and the absolute number of ghost tracks is lower for CATS, on condition that CATS reconstructs many more soft tracks. Table 4.3 shows reconstruction efficiencies for all types of reference tracks for $J/\Psi \rightarrow \mu ^+\mu ^-$ events mixed with 5 superimposed inelastic events.

Table 4.3: Reconstruction efficiencies and clone/ghost rates obtained on simulated $J/\Psi \rightarrow \mu ^+\mu ^-$ events mixed with 5 superimposed inelastic events for CATS, RANGER, TEMA packages for realistic scenario.

		Efficiencies (%)
Set	CATS	RANGER	TEMA
Ref. $J /\Psi$	95.5	89.1	81.5
Ref. Prim.	93.1	87.7	77.1
Ref. Tracks	90.5	82.1	74.4
All Tracks	60.1	41.2	39.8
Extra	43.3	17.3	20.6
Clone	5.	4.8	1.8
Ghost	18.4	21.6	22.8
MC tracks per event	119	82	79

In order to understand the dependence of the track reconstruction performance on the track multiplicity, the reconstruction efficiency of reference tracks and the ghost level were measured with different numbers $N$ of superimposed inelastic interactions exactly mixed. On average, the number of reconstructable tracks per event scales linearly with the number of exactly mixed interactions, rising from 40 tracks for one interaction up to 320 for eight. For this test, RANGER was taken as a reference. The results are summarized in Fig. 4.8.

Figure 4.8: Reconstruction efficiency for reference tracks and ghost level versus the number of superimposed (exactly mixed) inelastic interactions

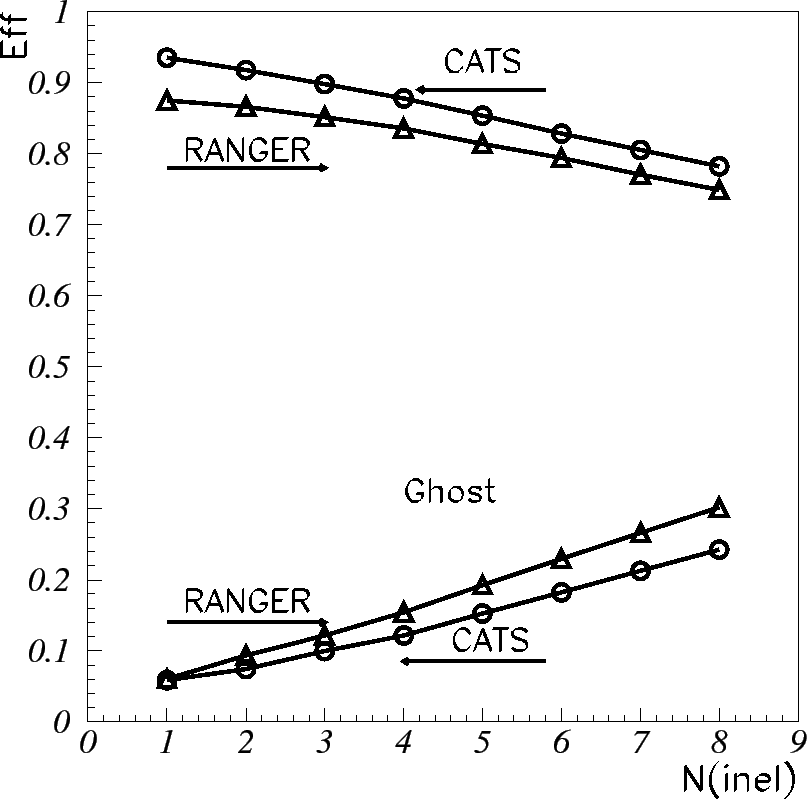While the mean interaction rate was expected to result in four Poisson distributed superimposed interactions, the performance of CATS was investigated for up to 8 interactions. The reconstruction efficiency for reference tracks slowly decreases from about 93% to 78%, ghost rate grows from 6% to 23%. As can be seen, the efficiency and ghost level of CATS show the same trends as those of RANGER demonstrating the stability and robustness of CATS.

In order to estimate the accuracy of the track reconstruction algorithm, track residual distributions are investigated at two planes: $z=z_f$ and $z=z_e$, where $z_f$, $z_e$ are the $z$-coordinates of the first and the last hits of the reconstructed track, respectively. The reliability of the track covariance matrix produced by the reconstruction algorithm is studied by investigating normalized residual distributions, using diagonal elements of the covariance matrix for normalization. By definition, the normalized residual (also called pull) of a track parameter, for instance $x$-coordinate, is

$$P(x) = \frac{\textstyle x^{REC} - x^{MC}}{\sqrt{\mathstrut\Gamma_{xx}}},$$

where $x^{REC}$ is the estimated value of $x$, $x^{MC}$ the value taken from Monte Carlo truth, $\Gamma_{xx}$ the corresponding diagonal element of the covariance matrix. Ideally, the distributions of pulls should be unbiased and have a Gaussian core of unity.

Table 4.4: Resolutions, pulls $P$ and mean length of reconstructed primary tracks.

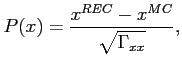
	CATS		RANGER		TEMA
Resolutions	OTR	ITR	OTR	ITR	OTR	ITR
$x$, $\mu$m	246	93	322	91	291	98
$y$, mm	3.7	1.4	5.0	1.4	4.1	1.4
$t_x$, mrad	0.62	0.24	0.71	0.24	0.76	0.26
$t_y$, mrad	4.73	1.79	6.96	1.79	5.39	1.87
Pulls
$P(x)$	1.59	1.11	1.37	1.10	1.45	1.06
$P(y)$	1.52	0.98	1.25	1.11	1.81	1.16
$P(t_x)$	1.16	0.93	1.25	0.89	1.18	1.15
$P(t_y)$	1.53	0.99	1.39	1.15	1.92	1.23
Hits/track	31	23	26	21	31	21

Table 4.4 presents values of pulls and residuals for four parameters $x$, $y$, $t_x$ and $t_y$ of properly reconstructed tracks and the mean length of the tracks given in the number of associated hits for all three algorithms.

The pulls in the OTR are typically wider than unity. As was mentioned in [#!ranger!#] wider pulls are caused by inevitably unresolved left/right ambiguities, hits picked up from other tracks, and a simplified treatment of multiple scattering. However, it should be mentioned, that this problem only affects the accuracy of track parameter estimates, leaving the track reconstruction efficiency untouched.

The efficiency of L/R ambiguity resolution in the OTR is investigated for three sets of tracks: lepton, primary and all reference tracks. The evaluation method was based on the comparison of the reconstructed sign of the drift radius $\widehat{q}$ with its true value $q$ taken from simulated data. Only significant errors in the L/R sign determination are taken into account, i.e. those for which the residual $\rho$ is

$$\rho=\left\vert\widehat{q}-q\right\vert\ge 3\sigma_0,$$

where $\sigma_0$ is the detector resolution. For each correctly reconstructed track (more than 70% of the hits belong to a certain simulated track) the fraction of L/R errors is calculated. The results are summarized in Table 4.5.

Table 4.5: Fractions of wrong L/R assignment in correctly reconstructed tracks.

Algorithm	CATS	RANGER	TEMA
Ref. $J/\psi$, %	1.9	4.6	3.7
Ref. Prim., %	2.9	4.4	3.9
All Refset, %	3.3	5.1	4.3

As can be seen, CATS provides the most accurate resolution of L/R ambiguities for all types of reference tracks.

Figure 4.9: Mean computing time per event versus the number of superimposed (exactly mixed) inelastic interactions.

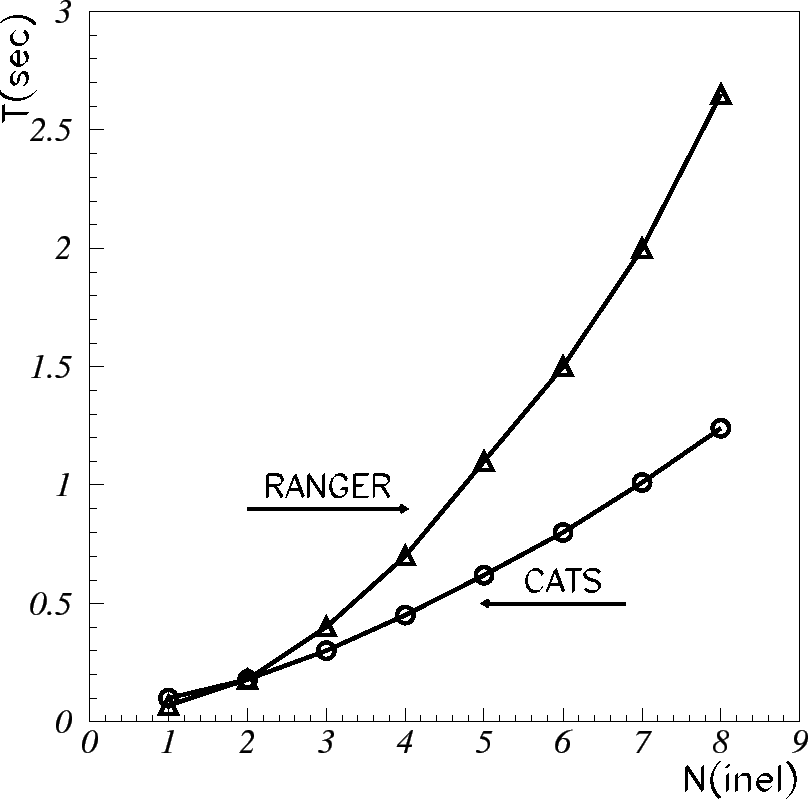A PC with dual 500 MHz CPU Pentium III processor was used to measure the time consumption of the algorithm. The mean CPU time needed for CATS to reconstruct an event with 2 mixed interactions was about 240 ms. The computing time dependence on the number of superimposed inelastic events for CATS and RANGER is shown in Fig. 4.9. For CATS, the CPU time consumption shows only a very moderate increase, corresponding to an almost constant time requirement per track. The main reasons for the observed computational superiority of CATS are

• the avoidance of combinatorial pile-up by hit clusterization in the OTR;
• the space-point based approach for track recognition performed by the cellular automaton;
• the fast algorithm for L/R ambiguity resolution;
• the optimized implementation of the Kalman filter.

Studies of $J /\Psi$ reconstruction efficiency on simulated $J/\Psi \rightarrow \mu ^+\mu ^-$ events mixed with 2 superimposed inelastic events, have shown that CATS provides an about 10% higher efficiency for $J /\Psi$ mesons than RANGER and 20% higher efficiency than TEMA with about the same mass resolution. CATS also has shown a higher efficiency for $K^0_S$ signal, it finds about 20% more $K^0_S$ than the other packages.