Test of the Algorithm with Monte Carlo

In order to estimate systematic errors and to define the accuracy of the hit efficiency measurement algorithm a special tool for Monte Carlo data tuning was used. This tool allows to apply efficiencies measured on MC data simulation. For the tests, the following mean efficiencies were used:

• 90% for chambers of the MS01 ,
• 80 % for chambers of the PC region,
• 80 % for chambers of the TC region.

Hits in the Inner Tracker chambers are produced according to the applied mean efficiencies. Neither global nor local misalignments for the ITR are applied.

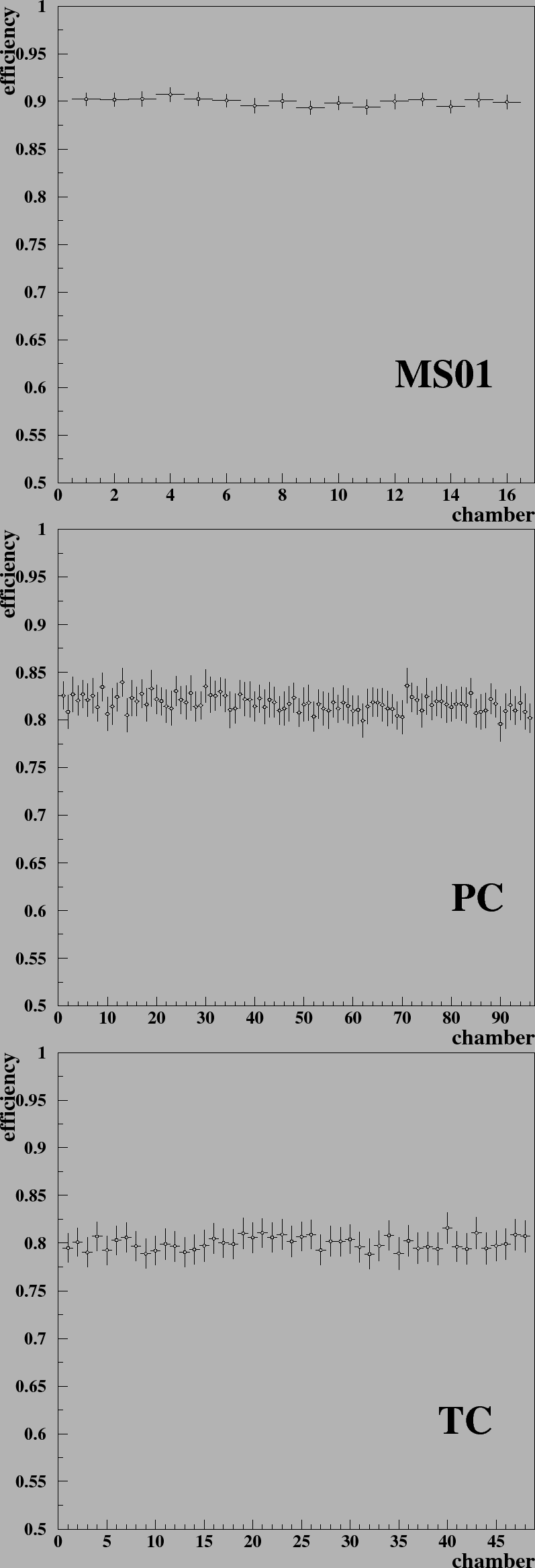
On MC the same algorithm for hit efficiency measurement is used as on real data. The selected sample of MC data contains 20.000 events and allows to achieve approximately 50.000 entries for each of MS01 chambers and 4.000 measurements for each of PC and TC chambers. The obtained results are shown in Fig. 5.14. There are three plots which illustrate the obtained efficiencies for MS01 superlayer, PC and TC area. The efficiencies are constant for MS01 within about 1% and compatible with the applied efficiencies. In the PC and TC chambers a deviation of about 2% are measured. These differences can be explained by the limited statistic. The obtained efficiency numbers are summarized in Table 5.2.

In order to check if the algorithm is able to deal with the ITR detector performances of 2002, with the large number of dead regions and observed low efficiency in PC region, a ``realistic scenario'' is applied:

1. for a particular run masks are produced and efficiencies for all chambers are calculated,
2. MIMPs^5.6 which are situated in the masked regions are discarded,
3. hits are produced from the MIMPs with a probability equal to the efficiencies measured on data for each chamber.

After applying efficiencies and masks, the standard routine for efficiency estimation is used. The obtained numbers are in agreement within about 2% with the efficiencies applied during simulation.

Figure 5.14: Hit efficiencies distribution obtained with Monte Carlo data for chambers of the Inner Tracker in the MS01 station, PC and TC area. Statistical errors are shown as error bars.

This shows that the pattern recognition program and the routine for efficiency estimation are robust enough to handle the real data and able to deliver reliable results.

Table 5.2: Mean efficiencies, efficiency variations and statistical errors obtained on Monte Carlo data with realistic settings.

	MS01	PC	TC
hit efficiency, $\%$	89.98	81.72	80.01
efficiency variation, $\%$	0.37	0.83	0.69
statistical error of efficiency, $\%$	2.2	5.03	4.78