Next: Summary of Used Cuts Up: Selection Previous: Selection Cuts Contents
The kinematic properties of the ![]() candidates can be illustrated by the
Armenteros-Podolanski plot. This is a two dimensional plot, of transverse
momentum
candidates can be illustrated by the
Armenteros-Podolanski plot. This is a two dimensional plot, of transverse
momentum ![]() of the oppositely
charged decay products with respect to the
of the oppositely
charged decay products with respect to the ![]() versus the longitudinal momentum
asymmetry
versus the longitudinal momentum
asymmetry
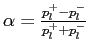 . The obtained distribution
(see Fig.6.4) can be
explained by the fact that decay products of the
. The obtained distribution
(see Fig.6.4) can be
explained by the fact that decay products of the
![]() have the
same mass and therefore their momenta are distributed symmetrically on average, while
for decays
have the
same mass and therefore their momenta are distributed symmetrically on average, while
for decays
![]() the proton (antiproton) takes on average a larger part of the momentum and as a
result the distribution is asymmetric.
the proton (antiproton) takes on average a larger part of the momentum and as a
result the distribution is asymmetric.
![]() are kinematically indistinguishable from
are kinematically indistinguishable from
![]() in
the area where the corresponding bands of the Armenteros-Podolanski plot overlap
and contribute to the background in the invariant mass distributions. A
simple cut allows to remove these overlaps: all
in
the area where the corresponding bands of the Armenteros-Podolanski plot overlap
and contribute to the background in the invariant mass distributions. A
simple cut allows to remove these overlaps: all ![]() and
and
![]() candidates are removed that fulfill a
candidates are removed that fulfill a ![]() mass hypothesis in the mass
range
mass hypothesis in the mass
range
![]() .
The loss of
.
The loss of ![]() signals due to the cut at the Armenteros-Podolanski plot is
approximately 10-15%. The bands in the Armenteros-Podolanski
plot can be explained by the applied mass cut.
signals due to the cut at the Armenteros-Podolanski plot is
approximately 10-15%. The bands in the Armenteros-Podolanski
plot can be explained by the applied mass cut.
Yury Gorbunov 2010-10-21