The Search for QGP

At sufficiently high temperature and density, the colour force between quarks becomes so small that they can behave as essentially non-interacting free particles. Therefore, if the conditions are extreme enough, the quarks should lose their confinement and a phase transition to a ``new'' form of matter should occur. This ``new'' form of matter is known as the Quark-Gluon Plasma (QGP) [#!qgp!#]. It is widely believed that with the help of heavy-ion colliders, it is possible to achieve this deconfined state. If so, a QGP system in a short time cools-down and re-hadronizes. The different stages are shown in Fig. 1.2.

Figure 1.2: The space-time evolution of a heavy-ion collision, which undergoes a phase transition to a QGP [#!lamot!#].

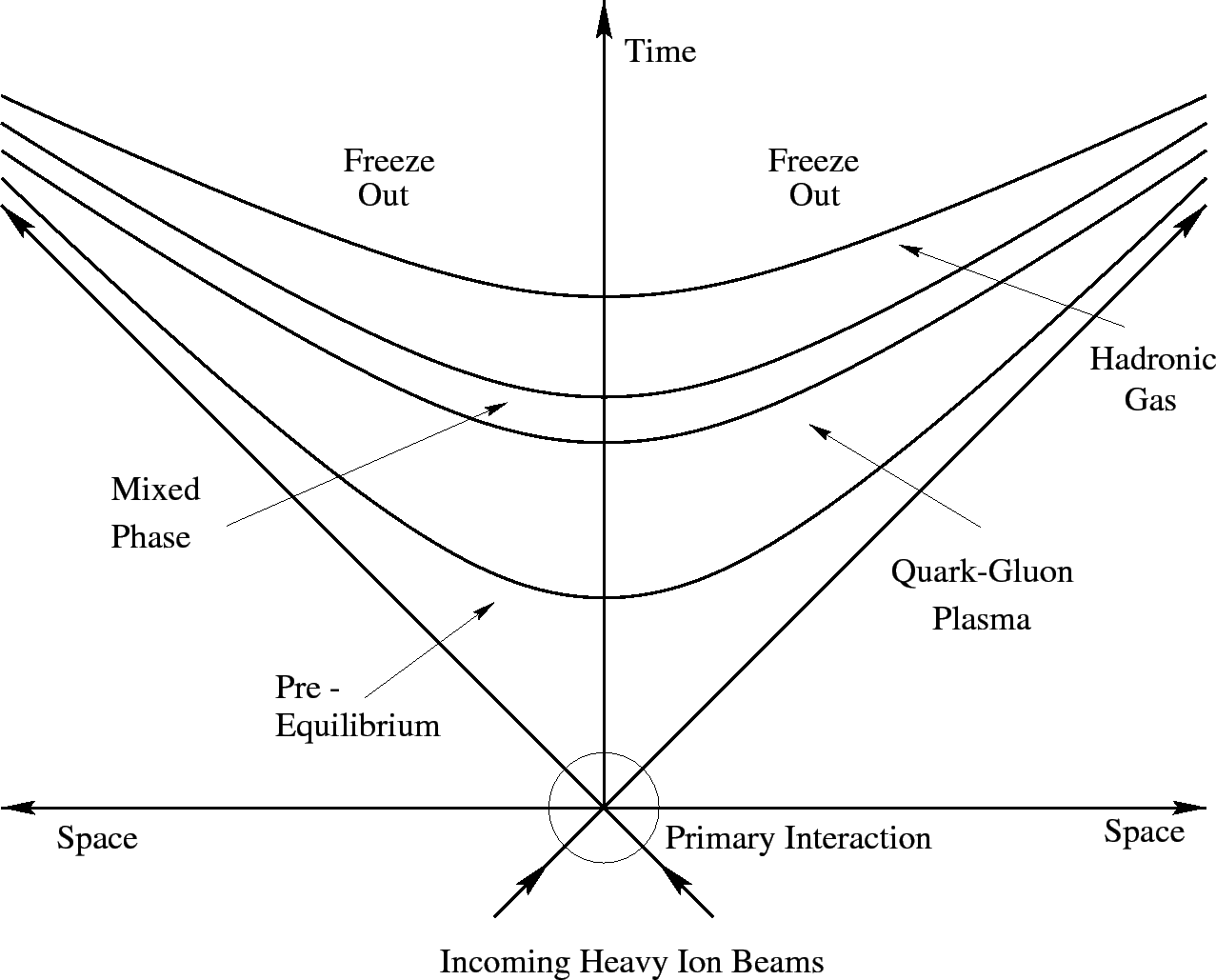The process is started when heavy-ion beams collide and a fireball is created. During an initial stage, many quarks and gluons are created in the collision volume in inelastic collisions. At the pre-equilibrium stage, these ``secondary'' partons interact with themselves. With the increase of parton density, $q\bar q$ pairs are created more easily due to the high temperature (Debye-screening process). When this partonic matter reaches equilibrium, it is called Quark-Gluon Plasma. At some point the fireball expands due to the internal pressure. It cools down and the system crosses the phase boundary, partons start to hadronize. At the end, the system expands until it is cool enough so that elastic collisions between particles can no longer occur and the particles' momenta are fixed.

As the deconfined phase is very short lived, it is impossible to detect it directly. Therefore, in order to conclude whether the phase transition occurred, the measurement of a quantity which is specific for the QGP phase is required.

The use of global observables, such as energy density as a function of temperature has a problem. A calculation of the energy density is model dependent and if the phase transition is continuous more than first order, the energy density will increase linearly with increasing temperature in the transition area. In order to avoid such a problem, other observables are used to search for a deconfined state of matter. It is predicted, that the phase transition can be seen experimentally in the following effects:

• Hard thermal dilepton/photon emission. Direct photons carry information about the thermodynamics of the QGP phase because their momentum distributions are determined by the temperature of the quarks, antiquarks and gluons in the plasma and because they are not affected by the hadronization. The momentum distributions of those photons should show an excess at higher transverse momenta, because the QGP should be formed at temperatures higher than those in the hadronic phase. Dileptons (lepton pairs: $e^{+},e^{-}$ and $\mu^{+},\mu^{-}$) also carry information about the thermodynamic properties of the fireball.

• Charmonium suppression. In a QGP phase, the $c\bar c$ pairs may become unbound due to the process of Debye-screening, which leads to a suppression in the measured yield of $J/\psi$. The process of Debye-screening occurs at high hadronic densities. A quark can interact with quarks of other hadrons, then the quark is not connected to a hadron and can propagate freely through a volume of deconfined quark and gluon matter.

• Strangeness enhancement. The production of strange and anti-strange quarks was proposed by Rafelski in 1982, as a probe to study the QGP phase transition. There are more available production channels for $s\bar s$ pairs in the QGP, due to the high gluon density and gluon fusion and annihilation of light $q\bar q$ pairs, then in ordinary $pp$ interaction. The gluonic channels contribute more than 80% to the total production rate for strange quarks.