Next: Acceptance Up: Selection Previous: Summary of Used Cuts Contents
Using the full chain of the detector simulation, track reconstruction and
![]() selection,
the resolution of the kinematic variables can be estimated. Fig. 6.5
shows residuals for kinematical variables
selection,
the resolution of the kinematic variables can be estimated. Fig. 6.5
shows residuals for kinematical variables ![]() and
and ![]() for
for
![]() and
and
![]() .
The Feynman scaling variable (
.
The Feynman scaling variable (![]() ) describes the longitudinal momentum
) describes the longitudinal momentum ![]() of the
scattering product, expressed in terms of the maximally possible momentum
of the
scattering product, expressed in terms of the maximally possible momentum ![]() ,
,
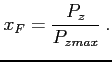 |
(6.1) |
| (6.2) |
| (6.3) |
| (6.4) |
The bin widths are chosen 0.015 for ![]() variable and 0.2
variable and 0.2
![]() for
for ![]() .
.
Yury Gorbunov 2010-10-21