V0 Reconstruction Using Fitting Techniques
A. C. Saulys
BNL
Work in Progress
Here are some PRELIMINARY results from my analysis of 99 HIJING central Au-Au
events from these files:
/star/rcf/test/gstardata/auau200/hijing135/jetq_on/b0_3/year_1b/hadronic_on/set0029_04_50evts.fzd
/star/rcf/test/gstardata/auau200/hijing135/jetq_on/b0_3/year_1b/hadronic_on/set0028_04_49evts.fzd
This is year 1 geometry, using tracks from TPC only refit using the Kalman
filter. I used SL99e (yes it is that old, but the ground did not rock while
I was developing the code).
Constraint fits to the V0 vertices and the impact parameter of the
daughter tracks at the primary vertex were done
using Victor's constrained fit code.
More details will be coming...
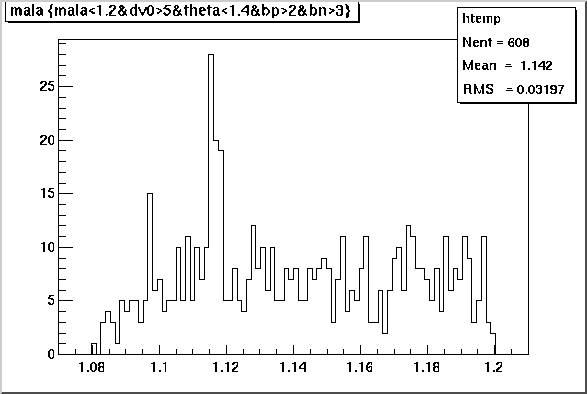
Effective mass spectrum of proton pi- with following cuts:
- Decay length > 5.0 cm
- Chisq/DF of impact at primary vertex (proton) > 2.0
- Chisq/DF of impact at primary vertex (pion) > 3.0
- Chisq/DF of V0 vertex with V0 constrained to point to primary vertex < 1.4
No Armenteros cuts, no magic, just basic physics principles and statistical
analysis used in the cuts.
Admitedly, the above figure has rather limited statistics, but a Lambda
signal above background can be calculated. The sum of the 4 bins with the
Lambda signal = 77.
Background from adjacent bins = 28. Number of Lambdas/event = .49 +- .06.
This should be compared with the corresponding number of .256 from
the nice work of Matt Lamont
where the traditional geometric cuts were used.
I think I may be able to improve on the background yet, but a background of
about 30% is not too bad.
My code is optimized for Lambda reconstruction (i.e. positive tracks are
fit as protons), but I do get the following K0s spectrum as a byproduct:
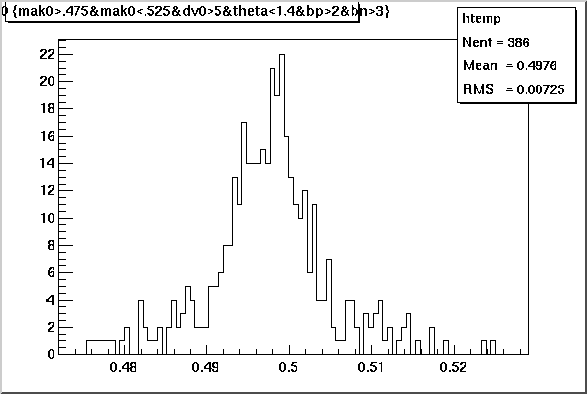
Effective mass spectrum of pi+ pi- with same cuts as above.
There are 386 K0s in that mass range and about 25% background (from adjacent bins), yielding
about 3 K0s/event as compared to 1.858 from Matt's work.
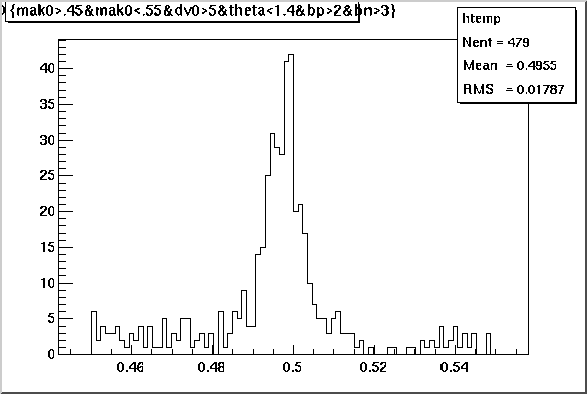
Effective mass spectrum of pi+ pi- with same cuts as above(with bigger mass range).
The advantages of my approach are not only that it yields more V0s/event,
but also the cuts are momentum independent, making corrections easier.
More to come...
Last update 2 March 2000



