



Next: About this document ...
Up: Hadron Single- and Multiparticle
Previous: Calculus of covariances
Contents
Kopytine's homepage
Generating sequences of random numbers with a fixed sum.
The multifireball event generator used in Chapter 7
is not a true event generator in the sense that it does not
propagate the initial state into a final state.
Rather, it generates a final state subject to a set of constraints.
The problem, expressed in the header of this Appendix,
had to be solved in order to
- impose momentum conservation on the final states created in the
multifireball event generator
- ensure independency of the event multiplicity on the mean
fireball size
Formulation of the problem: generate 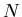 random numbers
random numbers
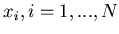 ,
subject to the condition
,
subject to the condition
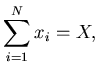 |
(114) |
so that the probability density distribution of an individual 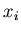 approaches given function
approaches given function
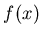 ( such that
( such that
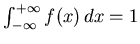 and the variance of
and the variance of 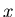 is finite) in the limit of large
is finite) in the limit of large 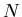 .
.
The multivariate probability density distribution can be presented
[83] as a product of conditional distributions
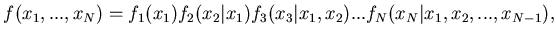 |
(115) |
where, e.g.,
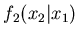 denotes distribution for
denotes distribution for 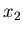 obtained from
obtained from
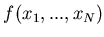 if one keeps
if one keeps 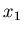 fixed at a certain value.
In the following, I will deliberately omit the normalization factor.
The extra complexity it brings in is not warranted in this context:
you get exactly one random number per subroutine call, therefore
normalization factor has no meaning
and only the functional shape of the distribution matters.
Here
fixed at a certain value.
In the following, I will deliberately omit the normalization factor.
The extra complexity it brings in is not warranted in this context:
you get exactly one random number per subroutine call, therefore
normalization factor has no meaning
and only the functional shape of the distribution matters.
Here
![$ {\mathfrak{D}}[x]$](img778.gif) is variance of
is variance of 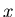 .
For the
.
For the 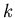 -th conditional distribution,
-th conditional distribution,
The last transition is based on an (approximate and non-rigorous !)
use of the Central Limit Theorem (CLT for short).
Indeed, having 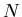 numbers
numbers 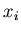 distributed according to
distributed according to 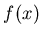 with
variance
with
variance
![$ {\mathfrak{D}}[x]$](img778.gif) and their sum being
and their sum being 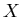 ,
one expects the sum
,
one expects the sum
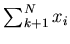 to be distributed around
to be distributed around
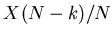 , with variance
, with variance
![$ (N-k){\mathfrak{D}}[x]$](img787.gif) .
Then,
.
Then, 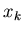 (the only free quantity other than
(the only free quantity other than
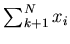 )
is distributed around
)
is distributed around
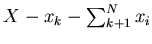 and the same variance,
since the total sum is strictly fixed at
and the same variance,
since the total sum is strictly fixed at 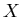 .
This use of CLT is
.
This use of CLT is
- non-rigorous because the CLT is valid for
independently sampled random numbers - in contradiction with
Eq. D.1.
- approximate because the CLT is a limit of large
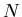 .
.
From the practical point of view, these caveats mean that for small 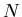 ,
the generated distribution of
,
the generated distribution of 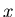 may deviate from
may deviate from 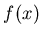 somewhat.
Nevertheless this technique accomplishes its goal whereas its approximate
nature is of no concern for the application in question.
somewhat.
Nevertheless this technique accomplishes its goal whereas its approximate
nature is of no concern for the application in question.




Next: About this document ...
Up: Hadron Single- and Multiparticle
Previous: Calculus of covariances
Contents
Mikhail Kopytine
2001-08-09
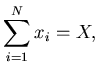
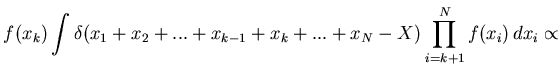
![$\displaystyle f(x_k)
\exp\left(-\frac{(\sum_1^{k-1}x_i+x_k+X(N-k)/N-X)^2}{(N-k)
{\mathfrak{D}}[x]}\right)$](img784.gif)