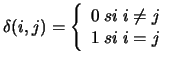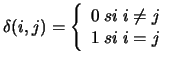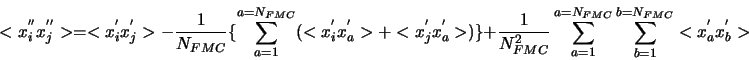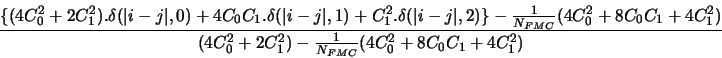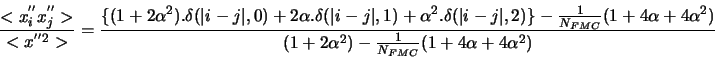Next: c - Quelques prédictions
Up: L'étude du couplage des
Previous: a - Définition des
Le modèle des corrélations de bruit est basé sur des hypothèses très simples. On suppose que le couplage est symétrique et ne dépend que de la distance entre les pistes. On appelle couplage avec le
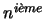 voisin le couplage entre la piste d'index i et les pistes d'index i+n et i-n si elles existent. Sans expliciter la nature des couplages entre les pistes, on peut le modéliser de la façon suivante: soit
voisin le couplage entre la piste d'index i et les pistes d'index i+n et i-n si elles existent. Sans expliciter la nature des couplages entre les pistes, on peut le modéliser de la façon suivante: soit 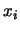 le signal de la piste i, on note le signal résultant du couplage aux
le signal de la piste i, on note le signal résultant du couplage aux
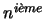 voisines
voisines
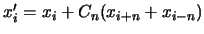 . D'une manière générale, le couplage d'une piste à ses voisines se note alors :
. D'une manière générale, le couplage d'une piste à ses voisines se note alors :
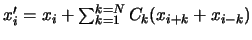 . Pour généraliser l'écriture et faciliter les calculs,
. Pour généraliser l'écriture et faciliter les calculs,
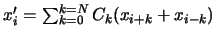 avec
avec 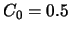 .
Il est possible de mener à terme les calculs analytiques du coefficient de corrélation moyennant quelques simplifications:
.
Il est possible de mener à terme les calculs analytiques du coefficient de corrélation moyennant quelques simplifications:
- Les signaux de base
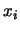 suivent la même loi de distribution dont la moyenne est nulle. En d'autres termes, le bruit est homogène sur toutes les pistes du détecteur. Les
suivent la même loi de distribution dont la moyenne est nulle. En d'autres termes, le bruit est homogène sur toutes les pistes du détecteur. Les 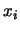 sont également décorrélés d'une piste à l'autre:
sont également décorrélés d'une piste à l'autre:
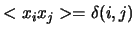 , où
, où 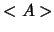 représente la valeur moyenne de A et
représente la valeur moyenne de A et
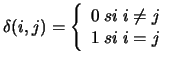
- Il est possible de construire le signal en trois étapes:
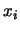 , le signal de base comme décrit auparavant.
, le signal de base comme décrit auparavant.
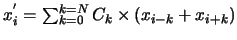 , signal couplé à ses voisins.
, signal couplé à ses voisins.
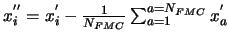 , le signal couplé corrigé de la fluctuation de mode commun.
, le signal couplé corrigé de la fluctuation de mode commun.
Dans ce cadre là,
Si on restreint le couplage aux premières pistes voisines uniquement,
D'où
Puisque
On obtient finalement :
si 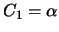 et
et 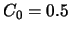 , la corrélation entre les pistes i et j devient:
, la corrélation entre les pistes i et j devient:




Next: c - Quelques prédictions
Up: L'étude du couplage des
Previous: a - Définition des
Walter Pinganaud 11 Octobre 2000