c - Quelques prédictions

Ce résultat est très riche en information sur le couplage des pistes. Ce cas très simple nous donne des tendances qui resteront vérifiées en dehors des hypothèses formulées. On peut d'ores et déjà faire trois observations:

On notera cependant que la corrélation résiduelle n'influe pas sur l'autocorrélation (lorsque i=j), en effet $Corr(i,i) = 1$, par définition du coefficient de corrélation.

La simulation des corrélations inter-pistes permet de vérifier la validité de ces résultats. Pour cela, les signaux sur les pistes sont distribués suivant une loi gaussienne centrée sur 0 et de RMS 10. La fluctuation de mode commun est également tirée, pour chaque événement, dans une gaussienne centrée sur zéro. Le couplage entre les pistes ne concerne que les deux premières voisines (à droite et à gauche). La figure 2.9 illustre la dépendance de la corrélation résiduelle au coefficient de couplage sur les premières voisines $\alpha$. Pour cette simulation, nous considérons un ensemble de 128 pistes. La corrélation résiduelle est extraite des simulations en moyennant la corrélation inter-piste pour des pistes séparées de plus de dix pas inter-pistes. L'expression analytique trouvée au préalable et la simulation donnent les mêmes résultats, il n'y a donc pas d'autres effets induits par la corrélation aux premières voisines ou par le calcul de la fluctuation de mode commun qui n'auraient pas été pris en compte dans le calcul. La corrélation résiduelle est de l'ordre de $-1\% \pm 0.4\%$ pour des couplages compris entre $\pm 10\%$.

Figure 2.9: Corrélation résiduelle en fonction du coefficient de couplage aux premières voisines.

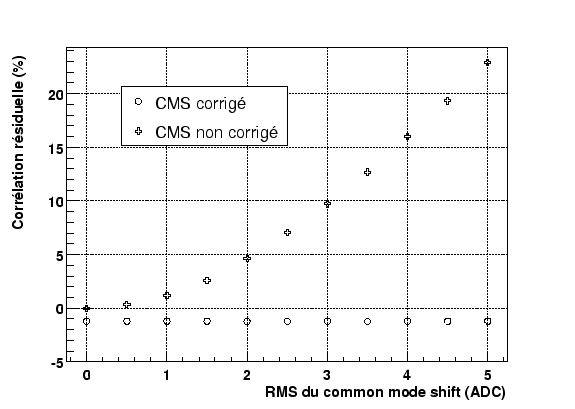
Comme nous l'avons démontré précédemment, la correction du signal par la fluctuation de mode commun induit une anticorrélation résiduelle. Cependant, si cette contribution n'est pas corrigée, elle conduit à des couplages résiduels qui peuvent être très importants comme indiqué sur la figure 2.10.

Figure 2.10: Corrélation résiduelle en fonction de la RMS de la fluctuation de mode commun (FMC ou CMS).

Ces résultats correspondent à un ensemble de 128 pistes dont les signaux suivent la même loi que précédemment, avec un couplage aux premières voisines de 5%. On note deux effets induits par cette fluctuation de mode commun: tout d'abord si elle est prise en compte, elle induit une anticorrélation résiduelle qui est indépendante de sa dispersion temporelle. D'autre part, si le signal n'est pas corrigé de cette fluctuation événement par événement, le couplage résiduel prend des valeurs qui croissent quadratiquement avec l'écart-type de la FMC. Cette corrélation atteint une valeur de 10% pour une dispersion de 3 coups ADC (qui est une valeur tout à fait envisageable comme nous l'avons vu). Les deux approches induisent donc une corrélation résiduelle. On préférera toutefois corriger systématiquement le signal pour éviter toute dépendance à la dispersion de la fluctuation de mode commun. Ceci permettra notamment de comparer des modules qui ont des écart-types de fluctuations de mode commun différents.

Il est important de caractériser la dépendance des coefficients de corrélation en fonction de la distribution du bruit sur les pistes. Dans ce but, nous allons procéder à trois études systématiques de l'impact du bruit dans le cadre du modèle simple qui a été exposé précédemment. Nous considérons un ensemble de 768 pistes qui ont un bruit moyen situé à 10 unités ADC et dispersé de façon gaussienne sur les pistes avec un sigma de 1. Chaque piste est couplée à ses deux premières voisines avec un coefficient de couplage de 5%.

• La première étude consiste à évaluer l'impact du pourcentage de pistes très bruyantes sur les coefficients de corrélation. Nous introduisons dans ce but, un pourcentage p de pistes ayant un bruit moyen de 100 dispersé autour de cette valeur avec un sigma de 4. La figure 2.11 représente l'évolution des coefficients de corrélation résiduelle et de corrélation aux premières voisines en fonction du pourcentage de pistes très bruyantes (de 0 à 100%).

  Figure 2.11: Evolution des coefficients de corrélation en fonction du pourcentage de pistes bruyantes.

  

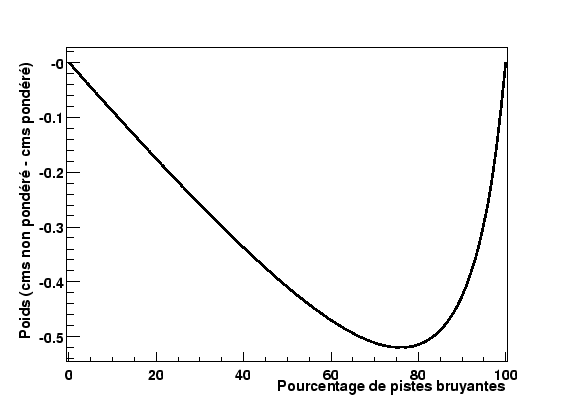
  La corrélation résiduelle est très stable et n'est pas dépendante du nombre de pistes bruyantes dans le détecteur. On remarque cependant que la corrélation aux premières voisines est stable jusqu'à environ 45% de pistes bruyantes puis augmente légèrement pour atteindre un maximum vers 70% puis décroître ensuite pour regagner sa valeur initiale. Ce comportement ne peut s'expliquer que par un calcul biaisé de la fluctuation de mode commun: une corrélation surévaluée est une caractéristique d'une mauvaise évaluation de la FMC. Dans le calcul de la fluctuation de mode commun, les signaux d'une puce sont pondérés par le bruit des pistes correspondantes. Ceci se justifie dans les cas où les pistes bruyantes sont minoritaires par rapport aux autres. Maintenant, si les pistes bruyantes sont majoritaires, cet argument n'est plus justifié car les pistes bruyantes correspondent à un comportement normal du détecteur. On peut confirmer cette observation en estimant le poids relatif des pistes ``non bruyantes'' dans le calcul de la FMC, en fonction du pourcentage de pistes bruyantes. La figure 2.12 représente la différence de ce poids calculé sans pondération et avec pondération, comme adopté jusqu'ici. L'écart entre ces deux poids atteint sont maximum pour 75% de pistes bruyantes.

  Figure 2.12: Ecart des poids des pistes non bruyantes (avec ou sans pondération) en fonction du pourcentage de pistes bruyantes.

  

  Il faut donc retenir que la méthode de pondération choisie convient bien à des cas où la proportion de pistes bruyantes n'est pas trop importante. Dans le cas contraire, cette situation conduit à une mauvaise évaluation de la fluctuation de mode commun qui entraîne une surestimation du coefficient de corrélation.

• Il est également important de contrôler la dépendance des coefficients de corrélation à la valeur du bruit sur les pistes. Pour cela, nous avons imposé à toutes les pistes une valeur du bruit variant de 0 à 100, dispersée suivant une loi gaussienne de sigma 1. En théorie, les coefficients de corrélation sont normalisés par rapport au bruit, ce qui évite toute corrélation. C'est en effet ce que confirme la figure 2.13, puisque nous n'observons aucune dépendance significative, au bruit des pistes, de la corrélation résiduelle et du coefficient de corrélation aux premières voisines.

  Figure 2.13: Dépendance des coefficients de corrélation au bruit des pistes.