Introduction

Dans le cas du détecteur de vertex, la reconstruction des clusters, et leur regroupement en paires pour le SSD, est naturellement suivie d'une phase d'association des points d'impact des différentes couches de détecteurs au silicium entre eux et avec les points de la TPC. Lorsqu'il est réalisable, ce couplage permet de reconstruire le plus complètement possible la trace de la particule, ce qui conduit à une détermination plus précise des quantités physiques associées. Lorsque STAR fonctionne en mode nominal, les particules suivent des trajectoires que l'on peut en général approcher par des hélices de part la présence d'un champ magnétique parallèle à l'axe du faisceau. Une hélice est entièrement définie par la connaissance de quatre ensembles de paramètres:

L'intensité du champ magnétique:

Il permet de déterminer la courbure de l'hélice pour une impulsion transverse donnée.

L'impulsion de la particule:

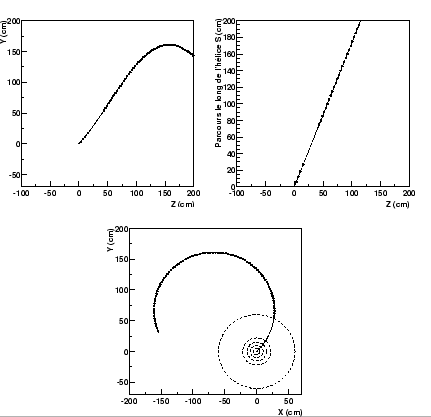
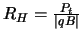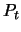Comme le montre la figure 4.1, la projection de l'hélice sur le plan (x,y) transverse à l'axe du faisceau est un arc de cercle de rayon $R_{H}=\frac{P_{t}}{\vert qB\vert}$ où $P_{t}$ est l'impulsion de la particule projetée sur le plan (x,y), 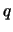$q$ est la charge de la particule et 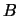$B$ l'intensité du champ magnétique.

Figure 4.1: Trois projections d'une hélice suivant les plans (Z,Y), (Z,S) et (X,Y).

La dernière composante de l'impulsion est extraite de la projection de l'hélice dans le plan (s,z) où s(x,y,z) est le chemin parcouru, par rapport à une origine arbitraire, par la particule. Dans ce référentiel, la trajectoire est une droite faisant un angle 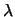$\lambda$ avec l'axe z. Le schéma 4.1 impose alors $P_{z}=P_{t}tan(\lambda)$.

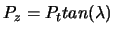Un point appartenant à l'hélice:

Ce point permet d'ancrer la trajectoire de la particule dans le référentiel global de STAR.

La charge de la particule:

Celle-ci détermine le sens de parcours de la particule le long de l'hélice.

La forme hélicoïdale idéale des trajectoires des particules est perturbée par des phénomènes tels que la diffusion coulombienne et la perte d'énergie des particules dans les matériaux traversés qui modifient le rayon de courbure de l'hélice.

Comme nous l'étudierons par la suite, la reconstruction de la trace dans la TPC nous permet d'extraire de façon précise l'impulsion de la particule grâce aux nombreux points qu'elle permet de mesurer (au minimum 45 pour une traversée complète du volume de la TPC). L'association des points du détecteur de vertex à cette trajectoire améliore quant à elle la résolution en position de la particule reconstruite. Dans ce qui suit, nous n'aborderons pas la présentation des techniques utilisées pour la reconstruction des trajectoires des particules chargées dans la TPC, mais nous insisterons sur les méthodes employées pour associer les points d'impact dans le détecteur de vertex aux traces de la TPC préalablement reconstruites. Plusieurs méthodes peuvent être envisagées pour parvenir à ce but, et nous présenterons les deux techniques qui sont effectivement utilisées par la collaboration STAR, selon leur ordre d'apparition.