Next: Track Fit by the Up: CATS Track Recognition Strategy Previous: Track Competition for Clone Contents
In this step it is assumed
that the track recognition is completed. Each track candidate is simply a sequence of
fired wires ![]() ,
,
![]() for which two problems have to be solved:
for which two problems have to be solved:
To solve both problems CATS uses a very promising approach that was proposed recently [#!CPC!#,#!NIM!#]. This approach is based on so-called elastic neural nets (ENN) [#!Durbin!#,#!Peterson!#] and generally employs the following heuristic idea:
In the presence of multiple scattering a track can be defined as the longest and the smoothest line which approaches the drift circles as close as possible.
Following this idea the problem of L/R ambiguity resolution and removal of outlying hits can be considered as an optimization problem in a form of either a variational problem or a problem of optimal trajectory control. Naturally, the optimization criterion is to be a sum of
Mathematically the ENN algorithm is an iterative numerical method to solve the given optimization problem. This method to solve L/R ambiguities has already successfully been applied to similar problems in [#!CPC!#,#!NIM!#]. The ENN in its elastic arm modification has also been studied by members of the HERA-B collaboration [#!Paus!#] where a full description and a detailed analysis of the method are presented.
Starting from the general ENN-based method to solve L/R ambiguities we describe a simplified version of the algorithm as implemented in CATS and applicable for relatively fast tracks.
The ENN algorithm employs a segment model for
track description: a track is considered as a sequence of neighboring straight-line
segments connecting nodes of the ENN -- points in 3D space which can change
their positions during iterations of the method. The ENN which is implemented in CATS
consists of two interacting arms (lower and upper ENNs in Fig. 4.7), each arm
includes ![]() nodes. The initial positions of the nodes on both ENN arms are chosen to
fully encompass a given sequence of drift circles around the
wires fired
nodes. The initial positions of the nodes on both ENN arms are chosen to
fully encompass a given sequence of drift circles around the
wires fired ![]() ,
,
![]() .
.
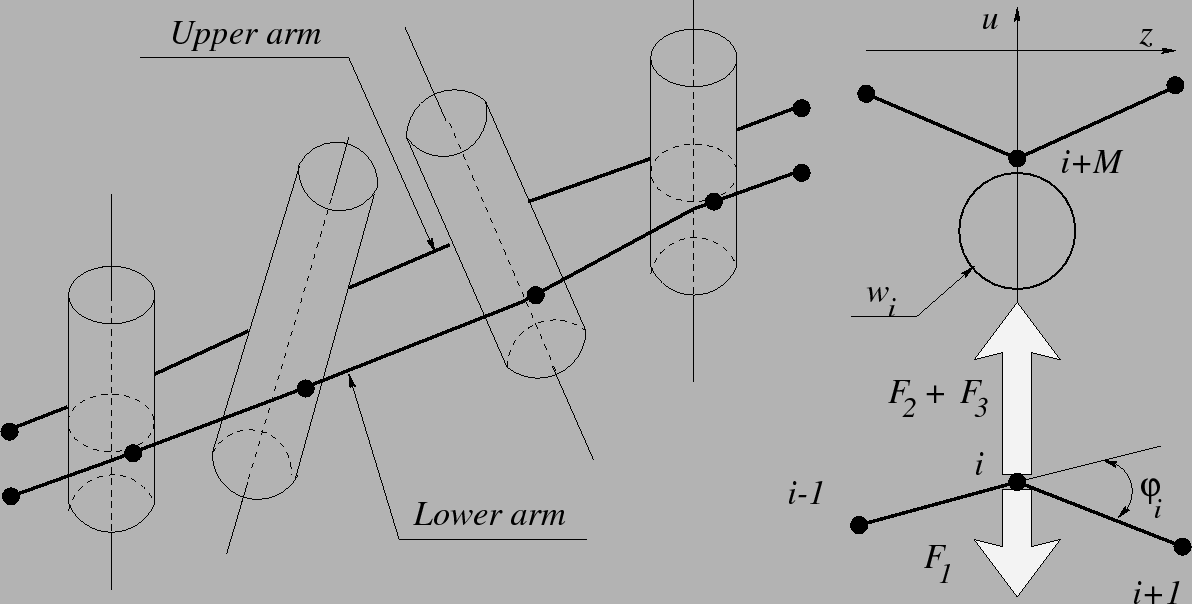 |
During an iteration an ENN node ![]() moves under the influence of three forces:
moves under the influence of three forces:
All three forces, ![]() ,
, ![]() , and
, and ![]() , depend on the mutual position of a
node, its counterpart in the other arm and the nearest drift circle. It is assumed
that the changes in the node's positions,
, depend on the mutual position of a
node, its counterpart in the other arm and the nearest drift circle. It is assumed
that the changes in the node's positions, ![]() , due to the different forces are described
by the following equations:
, due to the different forces are described
by the following equations:
In each iteration the positions of all nodes are updated according to the equation:
This approach is very general, it can, in principle, be applied to a wide spectrum of track reconstruction problems from reconstruction of straight, high-momentum tracks to fits of low-momentum hard scattered, even broken, tracks (the latter is the case in [#!CPC!#,#!NIM!#]). However, the algorithm can be simplified and made significantly faster, if the specific circumstances of the experiment are taken into account. CATS is dealing with relatively fast straight-line tracks. Most of the tracks which are of physics interest have momenta well above 1 GeV. Thus it is feasible to substitute a deformable segment-wise double ENN by a single straight-line rigid template.
The template's dynamics is described as a motion under the influence of an attraction force
pulling towards the drift circles. In order to suppress the influence of outlying hits
the force depends on the distance between the template and a drift circle decreasing
for large distances. Let
![]() be a vector of the
template's parameters at
be a vector of the
template's parameters at ![]() -th iteration. The algorithm
assigns two weight coefficients
-th iteration. The algorithm
assigns two weight coefficients ![]() and
and ![]() to each drift circle:
to each drift circle:
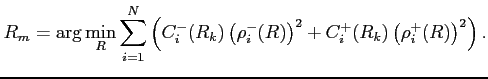
Studies on simulated data have shown that this algorithm provides remarkably high efficiency of the L/R ambiguity solution and very low level of noise hits. This is very important since an insufficient quality of L/R resolution and noise contamination in tracks can deteriorate the accuracy of the estimates produced by the Kalman refit of the reconstructed tracks.
Yury Gorbunov 2010-10-21