



Next: Role of T0
Up: Determination of the trigger
Previous: Determination of the trigger
Contents
Kopytine's homepage
The problem of absolute normalization
In nature, the probability for two nuclei to collide with impact
parameter between 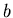 and
and 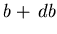 grows linearly with
grows linearly with 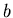 , and majority
of the collisions are peripheral.
In the experiment, the events to be recorded are selected by a trigger
which is sensitive to the event centrality via multiplicity of the
emitted particles.
A trigger can be described by its probability density of selecting an
event of certain total multiplicity.
In reality, this probability density will never have a sharp edge, and
the poorer the equipment, the more smeared will the edge be.
It is therefore best to characterize the centrality trigger
by giving the functional form of the total multiplicity distribution
it produces.
If this form is identical for two triggers, we will say that they belong
to the same centrality class.
, and majority
of the collisions are peripheral.
In the experiment, the events to be recorded are selected by a trigger
which is sensitive to the event centrality via multiplicity of the
emitted particles.
A trigger can be described by its probability density of selecting an
event of certain total multiplicity.
In reality, this probability density will never have a sharp edge, and
the poorer the equipment, the more smeared will the edge be.
It is therefore best to characterize the centrality trigger
by giving the functional form of the total multiplicity distribution
it produces.
If this form is identical for two triggers, we will say that they belong
to the same centrality class.
The problem of absolute normalization arises when one wants to obtain
the event averaged number of particles (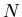 ) emitted
in the collision events of certain centrality (impact parameter) range,
or probability density distributions of particle emission with respect to
kinematical variables.
) emitted
in the collision events of certain centrality (impact parameter) range,
or probability density distributions of particle emission with respect to
kinematical variables.
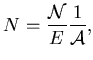 |
(18) |
where the desired average 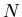 is calculated from the number
is calculated from the number
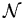 of detected
particle tracks over
of detected
particle tracks over 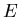 collision events of given trigger-selected
centrality class, using the apparatus which registers
only
collision events of given trigger-selected
centrality class, using the apparatus which registers
only
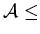 1
fraction of such tracks.
1
fraction of such tracks.
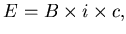 |
(19) |
where the 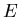 collisions are selected from the
collisions are selected from the 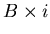 inelastic
beam-target interactions by means of the trigger.
The trigger is represented by quantity
inelastic
beam-target interactions by means of the trigger.
The trigger is represented by quantity 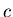 , which will be called
trigger centrality.
The interaction probability
, which will be called
trigger centrality.
The interaction probability 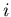 in eq. ( 4.17) is not
measured precisely.
Unknown in the eq. ( 4.17 ) is
in eq. ( 4.17) is not
measured precisely.
Unknown in the eq. ( 4.17 ) is
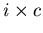 .
The beam count
.
The beam count 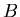 is live-gated and measured by the Cherenkov beam counter
(sections 3.5, 3.4.1, [29]).
In this section I quote
is live-gated and measured by the Cherenkov beam counter
(sections 3.5, 3.4.1, [29]).
In this section I quote 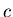 , assuming that
, assuming that 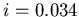 (as discussed in section
3.3).
(as discussed in section
3.3).
The 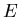 includes collisions with
and without tracks in the acceptance.
Important here is that even though the
includes collisions with
and without tracks in the acceptance.
Important here is that even though the 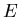 includes collisions
with no tracks in the acceptance, the requirement for them to be of the same
centrality class as the trigger events (to ensure ``cleanliness''
of the average (4.16)) forces one to pay attention to all
centrality-sensitive components of the trigger.
The notion of the
trigger-selected centrality class, or sample,
and its
characteristic
includes collisions
with no tracks in the acceptance, the requirement for them to be of the same
centrality class as the trigger events (to ensure ``cleanliness''
of the average (4.16)) forces one to pay attention to all
centrality-sensitive components of the trigger.
The notion of the
trigger-selected centrality class, or sample,
and its
characteristic 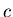 becomes therefore the key issue of the normalization
analysis.
becomes therefore the key issue of the normalization
analysis.
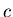 is the fraction of inelastic interactions, which includes all of
the following and only the following:
is the fraction of inelastic interactions, which includes all of
the following and only the following:
- (a)
- interactions that satisfy the trigger requirements
- (b)
- for every interaction of group (a), all interactions of
the same total multiplicity that happened in reality during the
run, but did not cause triggering due to absence of tracks in the
spectrometer's acceptance, and only due to this reason.
The class of events just described will be also referred
to as the ``normalization sample'' or ``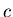 -sample''.
This definition of
-sample''.
This definition of 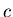 guarantees that the
guarantees that the 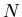 in formula (4.16)
is indeed the correct average multiplicity in the centrality class selected
by the trigger.
in formula (4.16)
is indeed the correct average multiplicity in the centrality class selected
by the trigger.
One should bear in mind that there is also a group of events which
do not
belong to the same total multiplicity class as the trigger events, have
acceptable T0 amplitude in the trigger
and do not create tracks in the spectrometer.
They must be excluded from the definition of the trigger-selected centrality
class and be not confused with the events of group (b) !
(Otherwise the result will be an underestimate of the true 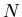 !).
This subtlety would not exist for a large acceptance experiment,
due to absence of the group (b) itself.
Among the mechanisms responsible for existence of the events with lower
total multiplicity but acceptable T0 amplitude are
!).
This subtlety would not exist for a large acceptance experiment,
due to absence of the group (b) itself.
Among the mechanisms responsible for existence of the events with lower
total multiplicity but acceptable T0 amplitude are
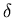 -electrons, noise and fluctuations
associated with operation of T0, fluctuations in the distribution of
charged tracks in space.
-electrons, noise and fluctuations
associated with operation of T0, fluctuations in the distribution of
charged tracks in space.
Let us list the centrality-sensitive components of the trigger and
briefly discuss them.




Next: Role of T0
Up: Determination of the trigger
Previous: Determination of the trigger
Contents
Mikhail Kopytine
2001-08-09
![]() ) emitted
in the collision events of certain centrality (impact parameter) range,
or probability density distributions of particle emission with respect to
kinematical variables.
) emitted
in the collision events of certain centrality (impact parameter) range,
or probability density distributions of particle emission with respect to
kinematical variables.
![]() includes collisions with
and without tracks in the acceptance.
Important here is that even though the
includes collisions with
and without tracks in the acceptance.
Important here is that even though the ![]() includes collisions
with no tracks in the acceptance, the requirement for them to be of the same
centrality class as the trigger events (to ensure ``cleanliness''
of the average (4.16)) forces one to pay attention to all
centrality-sensitive components of the trigger.
The notion of the
trigger-selected centrality class, or sample,
and its
characteristic
includes collisions
with no tracks in the acceptance, the requirement for them to be of the same
centrality class as the trigger events (to ensure ``cleanliness''
of the average (4.16)) forces one to pay attention to all
centrality-sensitive components of the trigger.
The notion of the
trigger-selected centrality class, or sample,
and its
characteristic ![]() becomes therefore the key issue of the normalization
analysis.
becomes therefore the key issue of the normalization
analysis.
![]() is the fraction of inelastic interactions, which includes all of
the following and only the following:
is the fraction of inelastic interactions, which includes all of
the following and only the following:
![]() !).
This subtlety would not exist for a large acceptance experiment,
due to absence of the group (b) itself.
Among the mechanisms responsible for existence of the events with lower
total multiplicity but acceptable T0 amplitude are
!).
This subtlety would not exist for a large acceptance experiment,
due to absence of the group (b) itself.
Among the mechanisms responsible for existence of the events with lower
total multiplicity but acceptable T0 amplitude are
![]() -electrons, noise and fluctuations
associated with operation of T0, fluctuations in the distribution of
charged tracks in space.
-electrons, noise and fluctuations
associated with operation of T0, fluctuations in the distribution of
charged tracks in space.