In our work,
a power spectrum analysis of event texture in pseudorapidity,
![]() and azimuthal angle
and azimuthal angle ![]() based on a
Discrete Wavelet Transformation (DWT)[17], is
performed on a number of large event ensembles sampled according
to their multiplicity, thereby studying the impact parameter dependence
of the observables.
DWT quantifies contributions of different
based on a
Discrete Wavelet Transformation (DWT)[17], is
performed on a number of large event ensembles sampled according
to their multiplicity, thereby studying the impact parameter dependence
of the observables.
DWT quantifies contributions of different ![]() and
and ![]() scales
into the overall event's texture, thus testing for possible
large scale enhancement.
scales
into the overall event's texture, thus testing for possible
large scale enhancement.
DWT formalizes the images
of the ![]() collision events in pseudorapidity
collision events in pseudorapidity ![]() and azimuthal
angle
and azimuthal
angle ![]() by expanding them into a set of functions orthogonal with
respect to scale and position in the (
by expanding them into a set of functions orthogonal with
respect to scale and position in the (![]() ,
, ![]() ) space, and allows one
to accumulate the texture information
by averaging the power spectra of many events.
While
the DWT analyzes the object (an image, a sequence of data points, a
data array) by transforming it,
the full information content inherent in the object is preserved
in the transformation.
Mathematically, this is expressed by stating that the discrete wavelet
family of functions constitutes a complete basis in the space
of all measurable functions defined on the continuum of real
numbers
) space, and allows one
to accumulate the texture information
by averaging the power spectra of many events.
While
the DWT analyzes the object (an image, a sequence of data points, a
data array) by transforming it,
the full information content inherent in the object is preserved
in the transformation.
Mathematically, this is expressed by stating that the discrete wavelet
family of functions constitutes a complete basis in the space
of all measurable functions defined on the continuum of real
numbers
![]() .
.
![]() This statement is known as the multiresolution theorem and constitutes
the theoretical ground for the multiresolution analysis.
This statement is known as the multiresolution theorem and constitutes
the theoretical ground for the multiresolution analysis.
The simplest DWT basis is the Haar wavelet, built upon the scaling function
![]()
![]() for
for ![]() and 0 otherwise.
If the interaction vertex lies on the detector's symmetry axis,
every pad's acceptance is a rectangle in the
and 0 otherwise.
If the interaction vertex lies on the detector's symmetry axis,
every pad's acceptance is a rectangle in the
![]() space.
Then, the Haar basis is the natural choice, as its scaling function in
two dimensions (2D)
space.
Then, the Haar basis is the natural choice, as its scaling function in
two dimensions (2D)
![]() is just a pad's acceptance (modulo units).
We therefore set up a 2D wavelet basis:
is just a pad's acceptance (modulo units).
We therefore set up a 2D wavelet basis:
| (87) |
| (88) |
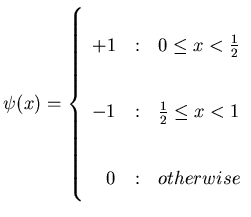 |
(89) |
We adopt the existing [19] 1D DWT power spectrum analysis
technique and expand it to 2D.
The track density in an individual event is
![]() and its local fluctuation
in a given event is
and its local fluctuation
in a given event is
![]() where
where
![]() is the average
is the average ![]() (over the acceptance)
in the given event.
(over the acceptance)
in the given event.
![]()
Using completeness of the basis, we expand
| (90) |
Notice that
![]() ,
being constant
within detector's
rectangular acceptance,
is orthogonal
to any
,
being constant
within detector's
rectangular acceptance,
is orthogonal
to any
![]() with
with ![]() .
Due to the
orthonormality condition
.
Due to the
orthonormality condition
![]() ,
the
,
the
![]() components for
different scales do not form cross-terms in the
components for
different scales do not form cross-terms in the ![]() sum,
and the sum
contains no cross-terms between
sum,
and the sum
contains no cross-terms between ![]() and
and
![]() for the four
observable scales.
Instead of a
for the four
observable scales.
Instead of a
![]() set, the
Si detector energy amplitude array
- its closest experimentally achievable approximation - is used as the
DWT input.
We used WAILI [81] software library to obtain the wavelet
decompositions.
set, the
Si detector energy amplitude array
- its closest experimentally achievable approximation - is used as the
DWT input.
We used WAILI [81] software library to obtain the wavelet
decompositions.
The Fourier power spectrum of a random white noise field
is known to be independent of frequency [80].
We are looking for dynamical textures in the data, and therefore
would like to treat the random white noise case as a ``trivial'' one
to compare with.
Therefore it is interesting to reformulate this property for
wavelets, where scale plays the same role as frequency in Fourier
analysis.
To do that, we link scales with frequencies, or in other words,
we must understand the frequency spectra of the wavelets.
The Fourier images of 1D
wavelet functions occupy a set of wave numbers
whose characteristic broadness grows with scale fineness ![]() as
as ![]() ;
;
![]() should be used in the 2D case.
Discrete wavelets of higher orders have better frequency localization
than the Haar wavelets.
Despite this advantage, we use Haar because only Haar allows
one to say that the act of data
taking with the (binned !) detector constitutes the first stage of the
wavelet transformation.
should be used in the 2D case.
Discrete wavelets of higher orders have better frequency localization
than the Haar wavelets.
Despite this advantage, we use Haar because only Haar allows
one to say that the act of data
taking with the (binned !) detector constitutes the first stage of the
wavelet transformation.
In 2D, we find it most informative to present the three modes of a power
spectrum
with different directions of sensitivity
![]() ,
,
![]() ,
, ![]() separately.
We define the power spectrum as
separately.
We define the power spectrum as