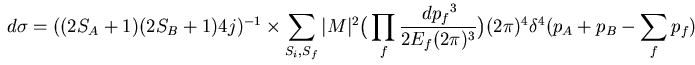- ... SPS
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- SPS - Super Proton Synchrotron, located at CERN
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (2D)
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- we denote azimuthal angle by
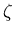 to reserve
to reserve 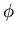 and
and 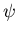 for the wavelet functions
for the wavelet functions
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ensembles
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- ... this is not the first DWT power spectrum analysis
performed on experimental data in the physics
of high energy hadron collisions - to my knowledge,
the first one was performed on a couple of
JACEE cosmic ray events in work [6].
The scarce event statistics left the feature eduction
potential of the DWT power spectrum underutilized.
Another difference from our case is that
only a 1D pseudorapidity-bound DWT was used in that work.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...):
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- With the normalization technique actually used, the accuracy of this
estimate does not affect the accuracy of the normalized particle yields, and
the estimate is given here for orientation only.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... observation
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- The acceptance is narrow and not every event produces
tracks in the spectrometer!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... pad
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
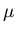 is defined for each pad in a sample of events.
is defined for each pad in a sample of events.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 1
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
-
An estimate for orientation: for Poissonian distribution of hits,
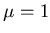 means that probability of having 1 or more hits is
means that probability of having 1 or more hits is
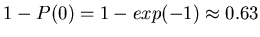 ,
i.e. the detector, in fact, is merely semi-occupied.
,
i.e. the detector, in fact, is merely semi-occupied.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- Their peculiar ``banana'' shape in the
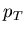 and
and 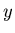 variables
is due to the constraint, imposed on
variables
is due to the constraint, imposed on 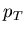 and
and 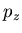 by constancy of momentum
by constancy of momentum 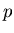 :
:
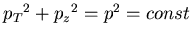 , and,
differentiating,
from
, and,
differentiating,
from
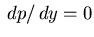 one gets
one gets
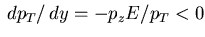 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... system
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- With '94 and '95 data, H4 was not yet used in
the
offline analysis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... section.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- By mid 1990s, after the long years of service, the scintillator's
transparency became reduced by radiation damage to a level which severely
undermined independence of the signal on the impact position along the face
of the stack. I had to correct for that problem - more on this in
section 4.4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... pions
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- In UCAL, 1-10 MeV neutrons from the nuclear break-ups in hadronic
showers do not go unnoticed but induce fissions. These fissions contribute to
the measured signal, thus rising it to a level typical for an electromagnetic
cascade caused by decay products of a
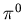 of the same energy.
of the same energy.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... channels
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- due to zero suppression
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... H4
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- Before the Pb run, H1 was replaced by
a pad chamber, but the nomenclature for the rest of the hodoscopes
was not changed
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... TIC
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- this multichannel Threshold Image
Cherenkov detector does not play any role in this analysis and I give no
special description of it. Its design and operation are described in
[37].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... production
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- The reason to choose this Lorentz-invariant
combination of quantities is the fact that
differential cross-section of an interaction of particles
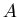 and
and 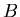 with
an arbitrary number of secondaries (indexed by
with
an arbitrary number of secondaries (indexed by 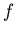 ) in the final state
is given by [39]
where
) in the final state
is given by [39]
where 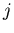 is an invariant flux,
is an invariant flux, 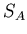 ,
, 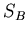 ,
, 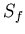 are spin quantum numbers,
and
are spin quantum numbers,
and 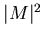 is the squared modulus of the invariant
amplitude of the process.
Therefore Eq. 4.1 represents the
is the squared modulus of the invariant
amplitude of the process.
Therefore Eq. 4.1 represents the 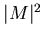 integrated over the phase space of the non-observed
particles, with certain coefficients.
integrated over the phase space of the non-observed
particles, with certain coefficients.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... range.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- This is supported by the existing data [41] on the
change of
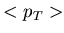 with
with 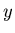 for primary negative hadrons.
As
for primary negative hadrons.
As 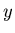 goes from 3.4 to 3.9,
goes from 3.4 to 3.9, 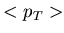 drops from
drops from
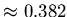
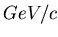 to
to
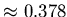
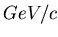 , i.e. by
, i.e. by
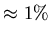 . Such an effect will not be
visible due to other larger error bars.
. Such an effect will not be
visible due to other larger error bars.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... factorized
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
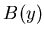 and
and 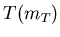 are defined by Eq. 4.8 itself.
Either one of them therefore can contain an arbitrary multiplier.
For our goals, this ambiguity is irrelevant, as will be clear from
the way
are defined by Eq. 4.8 itself.
Either one of them therefore can contain an arbitrary multiplier.
For our goals, this ambiguity is irrelevant, as will be clear from
the way 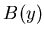 and
and 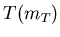 enter
Eq. 4.13 and Eq. 4.14.
enter
Eq. 4.13 and Eq. 4.14.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- This is the
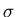 of the pion distribution according to RQMD and
also the
of the pion distribution according to RQMD and
also the 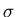 of the NA49's
of the NA49's 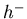 [41] distribution.
My attempts to determine
this parameter from our own pion data led me to conclude that this can only be
done with accuracy as poor as 50% because of narrowness of our coverage
in
[41] distribution.
My attempts to determine
this parameter from our own pion data led me to conclude that this can only be
done with accuracy as poor as 50% because of narrowness of our coverage
in 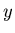 . The result however is consistent with NA49 and RQMD.
This remark applies to the kaons too.
. The result however is consistent with NA49 and RQMD.
This remark applies to the kaons too.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- As in RQMD.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... procedure
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- due to Michael Murray
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... extrapolating
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- here the artificial mass assignment is
equivalent to changing the integration variable within the
integral and does not change the result
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... area.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- The resulting
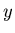 ranges are listed in Table 5.2.
ranges are listed in Table 5.2.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... be
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- assuming
that the dependence of the apparent inverse slope
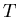 on the width is smooth enough so that it can be inter- and extrapolated
by the two points.
on the width is smooth enough so that it can be inter- and extrapolated
by the two points.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 1.4.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- The somewhat arbitrarily chosen number here is 99.7%.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... side
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- that is, the side of the detector, free of
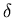 -electrons due to the deflecting effect of the dipole magnetic field.
-electrons due to the deflecting effect of the dipole magnetic field.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... DST
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- DST - the Data Summary Tape.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... path.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- In the subsequent event texture analysis, I extracted
the
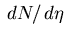 shape from the Si data. It was not different from that of
RQMD or HIJING.
shape from the Si data. It was not different from that of
RQMD or HIJING.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... beam
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- for the definition,
see Subsection 3.4.1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...sird_figure.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
-
A caveat: the above described correction method is not rigorous because the
simulation of effect is reduced to sampling from the distributions
of observed
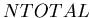 and
and 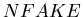 .
In the procedure,
.
In the procedure, 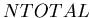 and
and 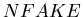 are being sampled independently
of each other.
Useful pairs of
are being sampled independently
of each other.
Useful pairs of 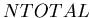 and
and 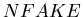 are only those where
are only those where
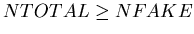 .
This means that the distribution of ``useful''
.
This means that the distribution of ``useful'' 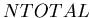 and
and 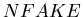 , which
will enter the correction procedure, will differ from the observable ones.
However, in practice, for a central trigger run, in most cases
, which
will enter the correction procedure, will differ from the observable ones.
However, in practice, for a central trigger run, in most cases
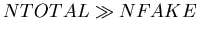 .
The result of this is that in case of the central runs, the bias coming
from the condition
.
The result of this is that in case of the central runs, the bias coming
from the condition
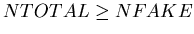 is negligible.
is negligible.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... hit
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- read out by Gasplex
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... scintillator.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- as discussed in detail in Appendix A
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... deterioration
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- An increase in the the sum/
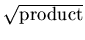 means that the attenuation
length decreases, see Appendix A.
means that the attenuation
length decreases, see Appendix A.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... threshold
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- This was not seen until I calibrated
out the position dependence of the UCAL signal, significant due to the
radiation damage in the scintillator (see Subsection 4.4.2).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- We neglect
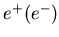 for the reasons outlined in
Subsection 4.4.3.
for the reasons outlined in
Subsection 4.4.3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... correction
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- Particles of different mass and life time have different acceptance
corrections, and they are calculated separately. By ``pionic'' one I mean the
one calculated for pions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... spectrometer,
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- data on momentum acceptance is found in Table 3.2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... counter
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- see section 3.4.1 for description
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...H3.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- see section 3.4.1 for description
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...counting
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- To emphasize: we do not have to identify, but merely
have to count the rejected kaons for this task.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... potential
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- parameter of statistical models needed to account for
the fact that the total baryon number in the system is fixed (conserved).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
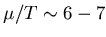
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- too high for the SPS freeze-out conditions,
but the authors of that early work
[20] considered lab energies
up to
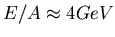
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Preliminary
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- To the best of my knowledge as of July 2001,
these NA49 data have not yet been published in the refereed press
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... midrapidity
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- from -0.5 to 0.5 in the CMS
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... triggered
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- we normally call it ``central trigger'', but in the field-off
situation this name is hardly justifiable, as seen from the context
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fits.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- This is not surprising for at least
two reasons: 1) a sample of events in a run is not a sample of
a constant
total multiplicity - the multiplicity varies event by event.
Thus varies the mean multiplicity
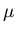 . A sum of multiple Poissonians
of different
. A sum of multiple Poissonians
of different 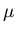 and arbitrary weights is not expected to be a Poissonian.
2) When the total multiplicity is fixed, the dominant reason for the
deviation will be correlations between particles (e.g. the Bose-Einstein
ones). In our case, however, the dominant reason is (1).
and arbitrary weights is not expected to be a Poissonian.
2) When the total multiplicity is fixed, the dominant reason for the
deviation will be correlations between particles (e.g. the Bose-Einstein
ones). In our case, however, the dominant reason is (1).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- In this Chapter, I denote azimuthal angle by
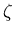 to reserve
to reserve
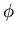 and
and 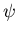 for the wavelet functions
for the wavelet functions
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...,
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
-
This value is
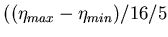 , i.e. 1/5 of the
pad's rapidity span.
, i.e. 1/5 of the
pad's rapidity span.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 0.01125.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- This value is 1/10 of the pad's rapidity span.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cross-talk
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- that is, the cross-talk between the given
stimulated channel
and all other channels of the chip
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... negative
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- that is, the induction has the opposite sign with respect to
the stimulating signal
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... theme
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- In the Discrete Wavelet Transformation approach, a very similar
problem - that of the
varying mean density
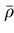 - is solved by virtue of the orthogonality
of the basis, as will be explained in section 6.6.
- is solved by virtue of the orthogonality
of the basis, as will be explained in section 6.6.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- remember that
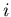 and
and 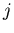 belong to the same half-ring and
are therefore close in
belong to the same half-ring and
are therefore close in 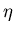
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... amplitudes
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- I am talking about calibrated amplitudes, where 0 corresponds
to the pedestal - hence ``positive'' and ``negative''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... positive.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- Incidentally, this is a good insight into the ``general
theory'' of correlation measures - a two point correlation approach
does not tell the whole story; one really needs a scale-differentiated
texture study !
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... midrapidity,
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- or, more accurately, towards pion midrapidity -
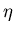 can
approximate
can
approximate 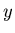 well for
well for 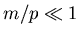
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
-
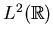 is the space of functions whose second power
is integrable:
is the space of functions whose second power
is integrable:
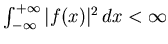 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... function
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- Some authors call it ``mother function''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... function.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- Some authors call it ``father function''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... event.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- In our notation, a scalar product of
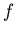 and
and 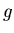 in the
in the
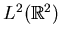 space is denoted as
space is denoted as
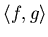 :
:
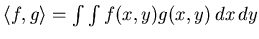 .
Repeated indices are being summed over, even if the summation symbol is
not written explicitly.
.
Repeated indices are being summed over, even if the summation symbol is
not written explicitly.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bin.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
-
The binning was done in the total ionization amplitude;
then charged multiplicity was assigned to those bins by dividing
total ionization by mean ionization of a pion with
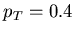 GeV/c.
GeV/c.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... data.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
-
Specifically, the following are probabilities for
a simulated particle to assume a particular identity:
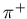 - 0.260;
- 0.260;
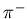 - 0.279;
- 0.279;
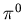 - 0.270;
- 0.270;
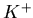 - 0.0635;
- 0.0635;
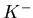 - 0.0317;
- 0.0317;
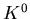 - 0.0952.
- 0.0952.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Gaussian
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- Not the most realistic one, it is chosen
because it enables fast and simple momentum-conserving
generation of random momenta.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- In this approach, one obtains particles
with a Gaussian
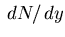 from a
superposition of multiple isotropic fireballs in a single event.
A single isotropic fireball can not produce a realistic combination
of
from a
superposition of multiple isotropic fireballs in a single event.
A single isotropic fireball can not produce a realistic combination
of 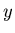 and
and 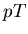 distributions.
distributions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sigma
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- Section 7.3
describes what they are
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... observables
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- We include flow observables
in the event-by-event class
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... problem.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
-
The NA49
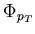 measurement[12] addressed the issue and
potentially could have revealed deviations from the local thermal equilibrium.
It had, however, no potential of proving the equilibrium due to the
logical
structure of the Central Limit Theorem upon which it rests[107]:
zero of the measure follows from the conditions interpretable as consistent
with equilibrium - but not other way round.
measurement[12] addressed the issue and
potentially could have revealed deviations from the local thermal equilibrium.
It had, however, no potential of proving the equilibrium due to the
logical
structure of the Central Limit Theorem upon which it rests[107]:
zero of the measure follows from the conditions interpretable as consistent
with equilibrium - but not other way round.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... compression
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- The DWT transformation in itself is not
yet a compression since the number of expansion coefficients necessary
to reconstruct the original image equals the number of original
pixels. The common DWT compression techniques are based on suppressing the
small expansion coefficients. The power spectrum (used in this work)
is based on a summation of squared expansion coefficients and thus,
effectively suppresses the impact of the small coefficients by
squaring everything, and at the same time reduces the amount of data
by the summation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... channel
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- in a dedicated run where natural
radioactivity of U is measured by the scintillator
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... calibrate.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
- if not for the light attenuation, it would have been
sufficient.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bins.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
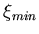 and
and 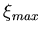 depend on
depend on 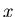 and on the
choice of binning.
and on the
choice of binning.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.