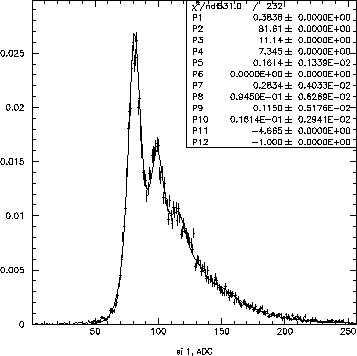
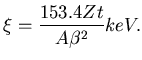Its distribution represents noise inherent in all
signal measurements.
Therefore, in the fitting model, this noise
distribution is folded with physical fluctuation of the ionization
energy loss.
The shape of the peak is non-Gaussian;
it has somewhat more events on the tails.
Therefore, I describe this peak by a product of a
Lorentzian (a function with pronounced tails), and a Gaussian
which prevents those tails from going too far.
The noticeable asymmetry of the peak is taken into account
in two ways: by introducing an addition of
an odd-power Hermite polynomial (with ![]() )
and by displacing the symmetry axis of the Lorentzian with
respect to that of the Gaussian (through
)
and by displacing the symmetry axis of the Lorentzian with
respect to that of the Gaussian (through ![]() ).
).
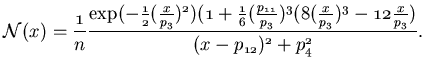 |
(56) |
The normalization constant ![]() has to be calculated numerically.
has to be calculated numerically.
![]() , where
, where ![]() is the ADC channel number and
is the ADC channel number and ![]() is the position
of the empty pad peak.
is the position
of the empty pad peak.
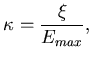 |
(57) |
where
![]() is the kinematical upper limit on the energy transfer in a single
collision:
is the kinematical upper limit on the energy transfer in a single
collision:
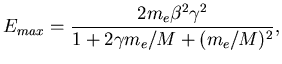 |
(59) |
where
In high energy physics, it is customary [78] to
use Landau distribution [76]
(which ignores the existence of ![]() ) for
) for
and use Vavilov distribution for
CERNLIB function DENLAN gives it as a function of a universal dimensionless
variable ![]() . This variable is related to the
actual energy loss,
. This variable is related to the
actual energy loss, ![]() , through the expression:
, through the expression:
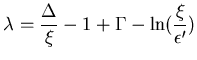 |
(61) |
Here ![]() is Euler's constant 0.577215... , and
is Euler's constant 0.577215... , and ![]() is explained by Eq. 6.5.
is explained by Eq. 6.5.
and ![]() is defined, according to Landau's work
[76], as
is defined, according to Landau's work
[76], as
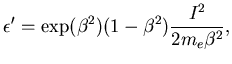 |
(62) |
where ![]() is ionization potential (of Si), taken to be 172.2 eV
on the basis of [77].
is ionization potential (of Si), taken to be 172.2 eV
on the basis of [77].
I set up the calibration code so that the Si thickness is calculated
taking into account the track's angle of incidence for given geometrical
location of a pad.
![]() is calculated for a "representative"
particle with
is calculated for a "representative"
particle with ![]() =0.4 GeV/c and
=0.4 GeV/c and ![]() .
.
The energy loss in the formula is related to the ADC channel X through
the conversion coefficient ![]() , and the "0" position
, and the "0" position ![]() .
.
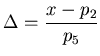 |
(63) |
![]() is the probability density of having
certain
is the probability density of having
certain ![]() , its integral = 1.
According to the expression above,
, its integral = 1.
According to the expression above,
![]() , therefore
the single particle ADC distribution
, therefore
the single particle ADC distribution
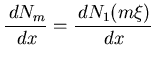 |
(64) |
Here is how the weights are related to the fit parameters
| (65) |
| (66) |
| (67) |
| (68) |
| (69) |
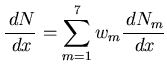 |
(70) |
This distribution is then folded with noise
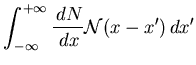 |
(71) |
Then I add the result (smeared compared to the "clean" Landau)
to the "0" peak
![]() .
.
-
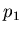 - the overall normalization, normally fixed at 1.
- the overall normalization, normally fixed at 1.
-
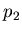 - position of the empty pad peak
- position of the empty pad peak
-
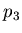 - Gaussian sigma of the empty pad peak
- Gaussian sigma of the empty pad peak
-
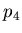 - Lorentzian gamma of the empty pad peak
- Lorentzian gamma of the empty pad peak
-
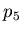 - ADC/keV conversion factor
- ADC/keV conversion factor
-
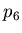 - makes parameters
- makes parameters 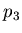 and
and 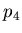 grow linearly with ADC,
normally set to 0.
grow linearly with ADC,
normally set to 0.
-
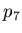 -
- 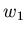
-
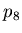 ,
,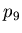 ,
,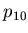 - used to define other weights
- used to define other weights
-
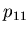 - Hermite polynomial asymmetry parameter
- Hermite polynomial asymmetry parameter
-
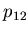 - Lorentzian asymmetry parameter
- Lorentzian asymmetry parameter