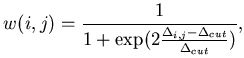Next: Cross-talk analysis
Up: Geometrical alignment of the
Previous: Formulation of the problem
Contents
Kopytine's homepage
Solution
From Eq.6.19, the criterion of the true coordinate
basis
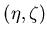 emerges naturally: it is the basis which
makes the observable
emerges naturally: it is the basis which
makes the observable
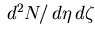 independent of
independent of 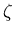 .
Such a criterion can be formulated quantitatively; then, the problem becomes
that of a formal minimization, treatable numerically.
This is done in the following way.
Let
.
Such a criterion can be formulated quantitatively; then, the problem becomes
that of a formal minimization, treatable numerically.
This is done in the following way.
Let 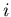 and
and 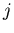 index pads.
We approximate acceptance of a pad
index pads.
We approximate acceptance of a pad 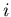 by a quadrangle and calculate its area
on the
by a quadrangle and calculate its area
on the
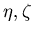 plane
plane 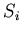 .
Then
.
Then
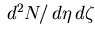 at the pad
at the pad 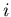 is approximated as
is approximated as 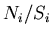 ,
where
,
where 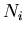 is the pad's mean occupancy.
We denote its statistical errorbar (based on the propagation of the fitting
error estimates obtained in the fitting procedure described in
6.3) as
is the pad's mean occupancy.
We denote its statistical errorbar (based on the propagation of the fitting
error estimates obtained in the fitting procedure described in
6.3) as
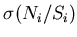 .
We seek an offset such that
.
We seek an offset such that
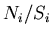 and
and 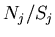 with
with 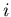 and
and 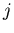 at different
at different 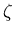 ,
but similar
,
but similar 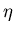 , be minimally different.
In practice, comparison of the
, be minimally different.
In practice, comparison of the 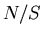 quantities must be limited to pads
with a finite
quantities must be limited to pads
with a finite
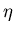 difference,
which is small enough so that the only reason for the difference of the
difference,
which is small enough so that the only reason for the difference of the 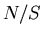 may be the geometrical offset.
Then, the quantity to minimize is
may be the geometrical offset.
Then, the quantity to minimize is
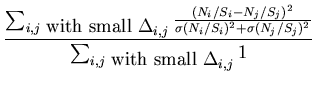 |
(73) |
where
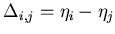 |
(74) |
is the maximal separation in 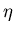 allowed.
Too small a value of
allowed.
Too small a value of
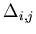 will result in too few channel pairs
to compare.
To calculate the function, a geometry transformation is required to
find displaced coordinates
will result in too few channel pairs
to compare.
To calculate the function, a geometry transformation is required to
find displaced coordinates
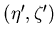 for every
for every
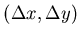 displacement of the detector in the vertical plane.
Displacement along the
displacement of the detector in the vertical plane.
Displacement along the 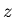 axis and rotations were not considered because the
problem does not seem sensitive to them.
GEANT simulation package [78]
was used to calculate the geometrical transformations,
and MINUIT
minimization package [79] - to search for the minimum of the
function given by formula 6.20.
At first, I was using
axis and rotations were not considered because the
problem does not seem sensitive to them.
GEANT simulation package [78]
was used to calculate the geometrical transformations,
and MINUIT
minimization package [79] - to search for the minimum of the
function given by formula 6.20.
At first, I was using
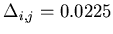 ,
,
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif) with a non-gradient
(SIMPLEX [79]) minimization.
Then I realized that the
function 6.20,
not everywhere differentiable,
could be made suitable for gradient minimization by smoothing it.
The smoothing was done by replacing the sharp cutoff at
with a non-gradient
(SIMPLEX [79]) minimization.
Then I realized that the
function 6.20,
not everywhere differentiable,
could be made suitable for gradient minimization by smoothing it.
The smoothing was done by replacing the sharp cutoff at
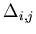 by a smoothly decaying weight function:
by a smoothly decaying weight function:
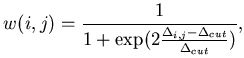 |
(75) |
where
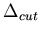 was set at 0.01125.
was set at 0.01125.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif) That is, the binary ``yes/no'' decision making on the inclusion
of a term was replaced by a weight, varying smoothly between 0 and 1.
That is, the binary ``yes/no'' decision making on the inclusion
of a term was replaced by a weight, varying smoothly between 0 and 1.
Figure 6.4:
Alignment results for run 3192. The axes show detector's offsets
in 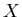 and
and 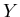 in cm. MIGRAD (see [79]) minimization
converged at point
in cm. MIGRAD (see [79]) minimization
converged at point
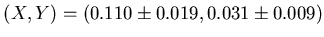 cm.
The dotted lines cross at the estimated minimum.
The contour and the errorbar estimates quoted correspond to the unit
deviation of the function from the minimum.
cm.
The dotted lines cross at the estimated minimum.
The contour and the errorbar estimates quoted correspond to the unit
deviation of the function from the minimum.
 |
A typical result of the minimization is shown on Figure 6.4.
The offsets we find are within the tolerance of the detector/beam
positions.
The
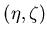 transformation so found was used in the Monte Carlo
detector response simulation to compare the measured
data with the event generators.
transformation so found was used in the Monte Carlo
detector response simulation to compare the measured
data with the event generators.




Next: Cross-talk analysis
Up: Geometrical alignment of the
Previous: Formulation of the problem
Contents
Mikhail Kopytine
2001-08-09
![]() emerges naturally: it is the basis which
makes the observable
emerges naturally: it is the basis which
makes the observable
![]() independent of
independent of ![]() .
Such a criterion can be formulated quantitatively; then, the problem becomes
that of a formal minimization, treatable numerically.
This is done in the following way.
Let
.
Such a criterion can be formulated quantitatively; then, the problem becomes
that of a formal minimization, treatable numerically.
This is done in the following way.
Let ![]() and
and ![]() index pads.
We approximate acceptance of a pad
index pads.
We approximate acceptance of a pad ![]() by a quadrangle and calculate its area
on the
by a quadrangle and calculate its area
on the
![]() plane
plane ![]() .
Then
.
Then
![]() at the pad
at the pad ![]() is approximated as
is approximated as ![]() ,
where
,
where ![]() is the pad's mean occupancy.
We denote its statistical errorbar (based on the propagation of the fitting
error estimates obtained in the fitting procedure described in
6.3) as
is the pad's mean occupancy.
We denote its statistical errorbar (based on the propagation of the fitting
error estimates obtained in the fitting procedure described in
6.3) as
![]() .
We seek an offset such that
.
We seek an offset such that
![]() and
and ![]() with
with ![]() and
and ![]() at different
at different ![]() ,
but similar
,
but similar ![]() , be minimally different.
In practice, comparison of the
, be minimally different.
In practice, comparison of the ![]() quantities must be limited to pads
with a finite
quantities must be limited to pads
with a finite
![]() difference,
which is small enough so that the only reason for the difference of the
difference,
which is small enough so that the only reason for the difference of the ![]() may be the geometrical offset.
Then, the quantity to minimize is
may be the geometrical offset.
Then, the quantity to minimize is