



Next: Calculus of covariances
Up: Hadron Single- and Multiparticle
Previous: Re-calibrating UCAL to correct
Contents
Kopytine's homepage
Subtracting background effects in the DWT power spectra.
This is a more technical discussion of the problem introduced in
Subsection 6.7.2, and the same notation is used.
The search for a good background subtraction technique underwent a
painfull involution from an ideal, but impossible, to an imperfect,
but doable.
Assuming that the interaction signals are a sum of the ``physics''
signal with the background distributed randomly according to 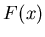 ,
the three distributions -
,
the three distributions -
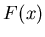 (non-interactions),
(non-interactions),
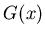 (minimum bias sample of interactions),
and
(minimum bias sample of interactions),
and 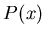 (``valid beam'' (
(``valid beam'' (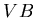 ) sample) -
are related in the following way :
) sample) -
are related in the following way :
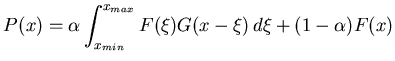 |
(102) |
Due to finiteness of binning, Eq. B.1
is, practically, a system of linear equations:
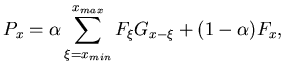 |
(103) |
where 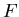 ,
,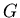 and
and 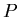 are normalized histograms
and
are normalized histograms
and 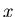 and
and 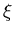 - discrete indices of bins.
- discrete indices of bins.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif) In principle, knowing
In principle, knowing 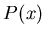 ,
, 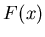 and
and 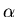 , one can try to determine
, one can try to determine
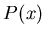 by solving this system of linear equations.
Our final goal, however, is correcting the average power spectrum components
(PSC).
by solving this system of linear equations.
Our final goal, however, is correcting the average power spectrum components
(PSC).
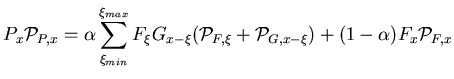 |
(104) |
This equation (B.3) reflects the fact that the mean of
the PSC distribution from the physics run is the weighted
sum of the PSC from the minimum bias interactions and from the empty target, and
that in the interaction events, the resulting PSC is a sum of PSCs from
``pure'' physics and background.
Having solved B.1 for 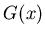 , one should solve
B.3 for
, one should solve
B.3 for
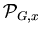 ,
whereby the background subtraction problem would be solved.
,
whereby the background subtraction problem would be solved.
This is the idealistic approach to background subtraction.
It can not be realized in practice because Eq. B.1 - Fredholm's
equation of the first kind - is a notorious ill-posed problem, whose solution
is, generally, numerically unstable.
This means that there is no hope of obtaining a physically meaningful
solution to Eq. B.1 in the practical situation with non-zero
errorbars.
Despite the fact that the solution to Eq. B.1 has been obtained
both numerically and using a symbolic processor such as MAPLE, it was
of no value because, typically, it was a non-physical oscillating function.
Therefore, the following simplfying assumption has been made.
The multiplicity binning is coarse enough so that the  of the
of the
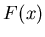 distribution is only about 1/3 of the bin size.
Therefore, approximation of
distribution is only about 1/3 of the bin size.
Therefore, approximation of 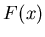 by a ``
by a ``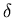 -function'' can be
easily justified:
-function'' can be
easily justified:
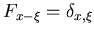 |
(105) |
This simplifies the system of equations B.2 to
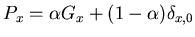 |
(106) |
In other words, the 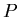 distribution is obtained from
distribution is obtained from 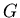 by increasing the
by increasing the 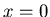 bin only.
Equations B.3 also become simpler, so that the solution for
bin only.
Equations B.3 also become simpler, so that the solution for
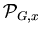 is easy:
is easy:
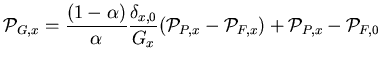 |
(107) |
Equation B.6 is already simple enough for
all bins but one, namely, the zero bin:
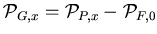 |
(108) |
This result could have been guessed intuitively.
For the zero bin, Eq. B.6 is not useful because 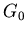 is not known.
is not known.




Next: Calculus of covariances
Up: Hadron Single- and Multiparticle
Previous: Re-calibrating UCAL to correct
Contents
Mikhail Kopytine
2001-08-09
![]() ,
the three distributions -
,
the three distributions -
![]() (non-interactions),
(non-interactions),
![]() (minimum bias sample of interactions),
and
(minimum bias sample of interactions),
and ![]() (``valid beam'' (
(``valid beam'' (![]() ) sample) -
are related in the following way :
) sample) -
are related in the following way :
![]() of the
of the
![]() distribution is only about 1/3 of the bin size.
Therefore, approximation of
distribution is only about 1/3 of the bin size.
Therefore, approximation of ![]() by a ``
by a ``![]() -function'' can be
easily justified:
-function'' can be
easily justified: