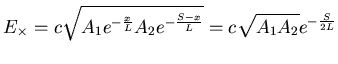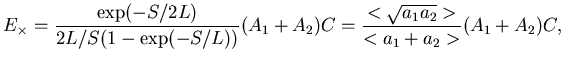Next: Subtracting background effects in
Up: Hadron Single- and Multiparticle
Previous: Bibliography
Contents
Kopytine's homepage
Re-calibrating UCAL to correct for the light absorbtion.
The algebra here provides technical background for
the material discussed in 4.4.2.
By 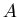 and
and 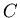 I denote the amplitude and calibration constant in
case of no light absorbtion, and by
I denote the amplitude and calibration constant in
case of no light absorbtion, and by 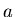 and
and 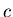 - the actual ones,
respectively.
If the light intensity in scintillator gets attenuated with distance
- the actual ones,
respectively.
If the light intensity in scintillator gets attenuated with distance 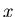 and the scintillator
length is
and the scintillator
length is 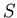 , then the amplitude observed in a single channel
(averaged over all positions in
, then the amplitude observed in a single channel
(averaged over all positions in 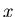 and eliminating the pedestal) is not
and eliminating the pedestal) is not 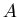 as it were in the absence of attenuation, but
as it were in the absence of attenuation, but
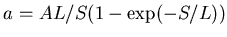 .
Each UCAL tower is served by two PMT tubes, so we have
.
Each UCAL tower is served by two PMT tubes, so we have  and
and 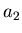 ;
their gains are matched so that
;
their gains are matched so that
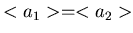 .
Calibrating a channel
.
Calibrating a channel ![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif) , I require that
, I require that
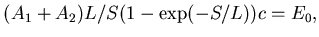 |
(98) |
where 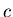 is to be determined and
is to be determined and 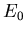 is known.
We will denote
is known.
We will denote
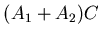 as
as 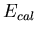 to indicate that this is
the energy observable which we know how to calibrate.
to indicate that this is
the energy observable which we know how to calibrate.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
The left and right PMT register the light which passes the distance 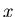 and
and 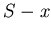 , respectively (if the source is point-like).
We use the product of the two so that our new observable is
, respectively (if the source is point-like).
We use the product of the two so that our new observable is
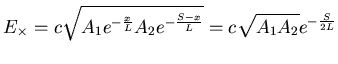 |
(99) |
It is independent of 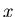 , but has yet to be calibrated, i.e.
related to
, but has yet to be calibrated, i.e.
related to 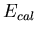 .
Next we notice that
.
Next we notice that
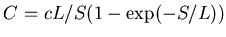 from A.1, and
that in the absence of absorption for the gain-matched tubes
from A.1, and
that in the absence of absorption for the gain-matched tubes
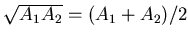 , and therefore
, and therefore
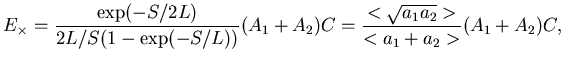 |
(100) |
where we recognized that the 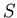 and
and 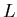 -dependent prefactor can be
expressed in terms of the easily measurable averages.
This means that calibration can be restored for the product with the help
of the expression:
-dependent prefactor can be
expressed in terms of the easily measurable averages.
This means that calibration can be restored for the product with the help
of the expression:
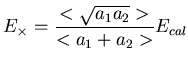 |
(101) |
By itself, this result is natural and predictable.
Its value lies in the fact that absorbtion length is now related to
observables.




Next: Subtracting background effects in
Up: Hadron Single- and Multiparticle
Previous: Bibliography
Contents
Mikhail Kopytine
2001-08-09
![]() and
and ![]() , respectively (if the source is point-like).
We use the product of the two so that our new observable is
, respectively (if the source is point-like).
We use the product of the two so that our new observable is