



Next: Si - spectrometer acceptance
Up: Determination of the trigger
Previous: General idea of the
Contents
Kopytine's homepage
Given the quality of the Si amplitude resolution in 1995, the traditional
method of multiplicity analysis, based on the channel-by-channel comparison
of amplitude with the MIP expectation, can not be reliably used for the
whole run period, because the amplitude resolution was affected by
radiation damage.
Multiplicity analysis can be performed under considerably relaxed
requirements to the amplitude resolution, if the probability distribution
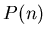 of number of tracks
of number of tracks 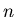 , crossing an individual pad of the array,
is known.
Our eventual goal, sufficient for the task of normalization as it is
formulated in the section 4.2.1, is finding a single number,
, crossing an individual pad of the array,
is known.
Our eventual goal, sufficient for the task of normalization as it is
formulated in the section 4.2.1, is finding a single number,
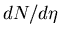 ,
characterizing the average multiplicity of the whole detector, averaged
over all events of a physics run.
Therefore it is acceptable to deal with one
,
characterizing the average multiplicity of the whole detector, averaged
over all events of a physics run.
Therefore it is acceptable to deal with one 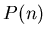 for the whole detector,
over the whole run (or a set of runs taken with a specific trigger
and angular setting).
Then, number
for the whole detector,
over the whole run (or a set of runs taken with a specific trigger
and angular setting).
Then, number 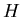 of the hit pads (
i.e., pads with signal above the threshold, set during
the calibration and subtracted during the DST
of the hit pads (
i.e., pads with signal above the threshold, set during
the calibration and subtracted during the DST
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif) -production)
out of
-production)
out of 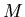 pads in total, is
pads in total, is
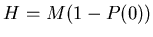 |
(21) |
As a measure of Si multiplicity, I use the Si occupancy calculated
event by event as
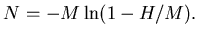 |
(22) |
Here 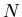 is the number of tracks that cross the array of
is the number of tracks that cross the array of 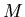 channels and
create
channels and
create 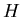 hits.
Equation 4.20 uses the Poisson law for
hits.
Equation 4.20 uses the Poisson law for 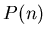 .
.
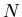 is linearly correlated with the total amplitude
(the sum of the channel amplitudes), and for low occupancy cases
I use the amplitude (properly calibrated in the units of
is linearly correlated with the total amplitude
(the sum of the channel amplitudes), and for low occupancy cases
I use the amplitude (properly calibrated in the units of 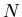 )
instead because in those cases contribution of
noise hits (due to drifting pedestals) or absent hits (again due to drifting
pedestals) may be significant.
)
instead because in those cases contribution of
noise hits (due to drifting pedestals) or absent hits (again due to drifting
pedestals) may be significant.
The multiplicity via occupancy expression (Eq. 4.20) has been
justified as an integral, or ``average'', multiplicity over the Si acceptance.
Variation of multiplicity from ring to ring is thus neglected.
The technical reason for that was the absence of individual ring
data in the existing DSTs.
If the track density is not uniform over the Si
acceptance, the formula results in a systematic error, which increases
for steeper
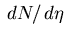 .
Let's compare the approximate expression for multiplicity
with the exact one.
.
Let's compare the approximate expression for multiplicity
with the exact one.
Approximate (Eq. 4.20 detailed):
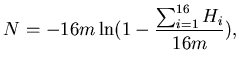 |
(23) |
where 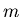 is number of pads in a ring,
is number of pads in a ring, 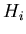 is number of hits,
and
is number of hits,
and 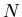 is the number of tracks crossing the detector.
is the number of tracks crossing the detector.
Exact:
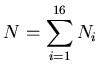 |
(24) |
where every
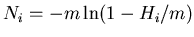 |
(25) |
- from every ring.
Therefore the exact formula is
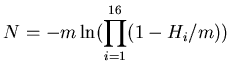 |
(26) |
To summarize, the approximate expression uses the arithmetic average in the
logarithm,
while the exact one replaces it by the geometrical average. We also see that
the approximate and exact expression become identical if
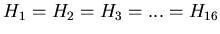 |
(27) |
i.e., if the distribution is uniform over the 16 rings of the detector.
Thus we see that knowledge of the distribution can serve to correct for the
systematic error. In principle there are two choices:
- purist: use real Si data to extract the shape of the distribution, and
use that information to get the correction.
- pragmatic: we know (and use this knowledge elsewhere in the analysis) that
RQMD reproduces the shape of the non-identified
charged  (and therefore
(and therefore
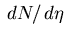 ) fairly well.
Compare, e.g., the NA49 data points in Fig 4.2
with the corresponding RQMD histogram plotted as a line.
) fairly well.
Compare, e.g., the NA49 data points in Fig 4.2
with the corresponding RQMD histogram plotted as a line.
Figure:
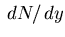 distributions for negative hadrons:
solid and open points - from NA49 measurements
[41];
the histogram - from
RQMD events of comparable centrality.
distributions for negative hadrons:
solid and open points - from NA49 measurements
[41];
the histogram - from
RQMD events of comparable centrality.
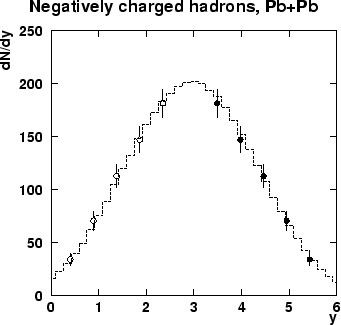 |
So, we can use RQMD to get the correction.
I followed the second path.
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif) The average number of tracks hitting
a pad in a specific ring can be extracted from a properly binned RQMD charged
track (
The average number of tracks hitting
a pad in a specific ring can be extracted from a properly binned RQMD charged
track (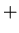 and
and 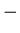 )
)
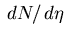 distribution:
distribution:
because 16 rings (with equal pseudorapidity coverage) of the detector
cover pseudorapidity range 1.5 to 3.3, and each
ring has 32 pads. Inverting Eq. 4.20,
the 16 values of 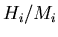 were
obtained - they range between 0.5 and 0.8. Plugging them into the ``approximate''
and ``exact'' expressions above yields the correction:
were
obtained - they range between 0.5 and 0.8. Plugging them into the ``approximate''
and ``exact'' expressions above yields the correction:
Conclusion: the multiplier 1.022 needs to be applied to
account for deviation of the
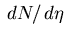 distribution from uniformity over the Si
acceptance.
distribution from uniformity over the Si
acceptance.




Next: Si - spectrometer acceptance
Up: Determination of the trigger
Previous: General idea of the
Contents
Mikhail Kopytine
2001-08-09
![]() .
Let's compare the approximate expression for multiplicity
with the exact one.
.
Let's compare the approximate expression for multiplicity
with the exact one.
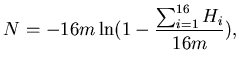
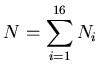
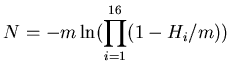
![]() (and therefore
(and therefore
![]() ) fairly well.
Compare, e.g., the NA49 data points in Fig 4.2
with the corresponding RQMD histogram plotted as a line.
) fairly well.
Compare, e.g., the NA49 data points in Fig 4.2
with the corresponding RQMD histogram plotted as a line.

![]() The average number of tracks hitting
a pad in a specific ring can be extracted from a properly binned RQMD charged
track (
The average number of tracks hitting
a pad in a specific ring can be extracted from a properly binned RQMD charged
track (![]() and
and ![]() )
)
![]() distribution:
distribution:
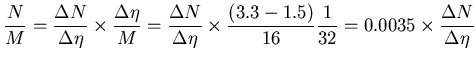
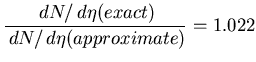
![]() distribution from uniformity over the Si
acceptance.
distribution from uniformity over the Si
acceptance.