Fig. 7.1 presents a comparison of the DWT dynamic texture
in the measured and RQMD-simulated ![]() collision events.
The three directional sensitivity modes
(diagonal
collision events.
The three directional sensitivity modes
(diagonal ![]() , azimuthal
, azimuthal ![]() , and pseudorapidity
, and pseudorapidity ![]() )
have four scales each, so that there are 12 sets of points
in the DWT dynamic texture as
a function of the charged multiplicity
)
have four scales each, so that there are 12 sets of points
in the DWT dynamic texture as
a function of the charged multiplicity
![]() bin.
bin.
![]() The systematic errors on the points (shown by vertical bars)
have been evaluated following the procedure described in detail in
Section
6.9.
The systematic errors on the points (shown by vertical bars)
have been evaluated following the procedure described in detail in
Section
6.9.
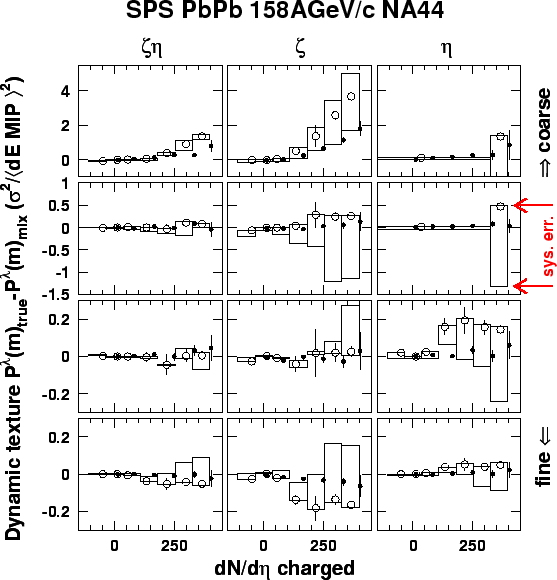 |
Fig.6.11
demonstrated that the major fraction
of the observed texture exists also in mixed events.
A detailed account of the causes was discussed in the preceding section
(Section 6.9)
, including known physics as well as instrumental effects.
It is therefore clear that the observable most directly related to the
dynamical correlations/fluctuations is not
![]() (introduced in 6.6)
, but
(introduced in 6.6)
, but
![]() .
We find that if one uses the concepts of fluctuation and scale
simultaneously, so that scale-local description of fluctuations is
possible, then the term ``correlation'' becomes redundant for describing
texture, because a ``correlation'' on some scale can always be thought of as
a ``fluctuation'' on a larger scale.
For example, density of paint on the surface of a chess board looks like
a ``correlation without fluctuation'' on the scale of each of its 64 fields,
and at the same time, as a ``fluctuation without correlation''
on the scale of the entire chess board.
Alternatively, if one uses the term ``correlation'' and specifies scale, then
the term ``fluctuation'' becomes redundant.
.
We find that if one uses the concepts of fluctuation and scale
simultaneously, so that scale-local description of fluctuations is
possible, then the term ``correlation'' becomes redundant for describing
texture, because a ``correlation'' on some scale can always be thought of as
a ``fluctuation'' on a larger scale.
For example, density of paint on the surface of a chess board looks like
a ``correlation without fluctuation'' on the scale of each of its 64 fields,
and at the same time, as a ``fluctuation without correlation''
on the scale of the entire chess board.
Alternatively, if one uses the term ``correlation'' and specifies scale, then
the term ``fluctuation'' becomes redundant.
 |
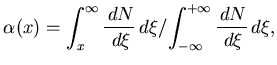 |
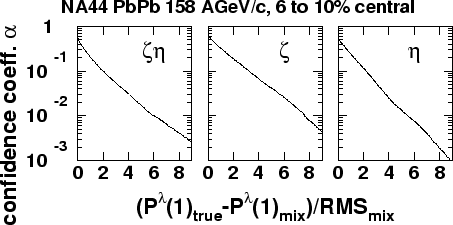
(93) |
The fluctuation strength observable provides a
limit on the frequency and strength of the fluctuations and expresses
the result in a model-independent way.
The confidence level
with which local fluctuations of a given strength (expressed through the
EbyE observables via Eq. 7.2)
can be excluded
is then ![]() .
Fluctuations greater than
.
Fluctuations greater than
![]() are excluded
in the azimuthal and pseudorapidity modes with 90% and 95% confidence,
respectively.
The monotonic fall of the curve is consistent with the absence of abnormal
subsamples in the data.
are excluded
in the azimuthal and pseudorapidity modes with 90% and 95% confidence,
respectively.
The monotonic fall of the curve is consistent with the absence of abnormal
subsamples in the data.
RQMD events were fed into the GEANT detector response simulation (Section 6.8) and analyzed using the same off-line procedure as used for the experimental data. The detector offset with respect to the beam center of gravity and the beam profile were included in the simulation. In a separate simulation run, the beam profile was identified as the cause of the rise of the azimuthal dynamic texture with the multiplicity on the coarse scale. In our experiment, this purely instrumental effect dominates the azimuthal component of the DWT dynamic texture.
The most apparent conclusion from Fig. 7.1 is that a large fraction of the texture (seen on Fig. 6.11) is not dynamic i.e. not different between true and mixed events. Being monotonic (or absent), the change of the data points with multiplicity does not reveal any evidence of a region of impact parameters/baryochemical potentials with qualitatively different properties, such as those of a critical point neighbourhood. The RQMD comparison confirms that particle production via hadronic multiple scattering, following string decays (without critical phenomena or phase transition) can explain the observed results when detector imperfections are taken into account. More detailed discussion of the implications of these data on various phase transition models will be given in Sections 7.4 and 7.5.