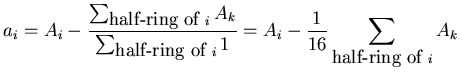Next: Cross-talk evaluation: results and
Up: Cross-talk analysis
Previous: Channel wiring and numbering
Contents
Kopytine's homepage
The covariance matrix approach
In our detector with 512 channels, there are
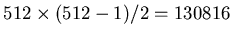 two channel pairs (unordered),
all of which were subjected to covariance analysis off-line.
A cross-talk, present between channels
two channel pairs (unordered),
all of which were subjected to covariance analysis off-line.
A cross-talk, present between channels  and
and  , and absent
in some other pairs, makes the
, and absent
in some other pairs, makes the 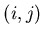 pair special in some respect.
The quantitative way to look at the problem, at first glance,
appears to be the following.
On a sufficiently large set of events
(statistics of a single run,
pair special in some respect.
The quantitative way to look at the problem, at first glance,
appears to be the following.
On a sufficiently large set of events
(statistics of a single run,
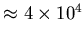 events
is sufficient)
calculate the covariance matrix of all channels:
events
is sufficient)
calculate the covariance matrix of all channels:
cov![$\displaystyle (A_i,A_j) = {\mathfrak{M}}[(A_i-{\mathfrak{M}}[A_i])(A_j-{\mathfrak{M}}[A_j])] ={\mathfrak{M}}[A_i A_j]-{\mathfrak{M}}[A_i]{\mathfrak{M}}[A_j],$](img561.gif) |
(76) |
where the
![$ \mathfrak{M}[\ ]$](img562.gif) is a mathematical expectation operator.
Its estimate is an average taken on a set of events.
When this is done, the pattern turns out to be dominated by the trivial
ring-wise correlation (with the covariance matrix having characteristic
chess-board structure, if the
is a mathematical expectation operator.
Its estimate is an average taken on a set of events.
When this is done, the pattern turns out to be dominated by the trivial
ring-wise correlation (with the covariance matrix having characteristic
chess-board structure, if the 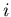 and
and 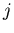 indices are assigned according
to the channel numbering described in subsection 6.5.2 above.
In other words, one sees that a correlation between channels
indices are assigned according
to the channel numbering described in subsection 6.5.2 above.
In other words, one sees that a correlation between channels
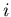 and
and 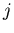 is the tighter, the closer their ring indices.
This turns out to be a manifestation of a recurrent theme
is the tighter, the closer their ring indices.
This turns out to be a manifestation of a recurrent theme
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif) in the study of correlations - a problem of the
varying mean density which feigns a correlation, when one looks at a
two-point correlator like the one of Eq. 6.23.
What happens is a departure of
cov
in the study of correlations - a problem of the
varying mean density which feigns a correlation, when one looks at a
two-point correlator like the one of Eq. 6.23.
What happens is a departure of
cov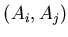 from 0 simply because
an event of a larger/smaller multiplicity tends to increase/decrease
from 0 simply because
an event of a larger/smaller multiplicity tends to increase/decrease
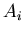 as well as
as well as 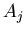 in a correlated way.
This correlation is genuine but trivial.
To go beyond it, one needs to identify/estimate
and subtract the varying part of
in a correlated way.
This correlation is genuine but trivial.
To go beyond it, one needs to identify/estimate
and subtract the varying part of 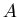 in some way.
The way we do it is by taking, for a given event, a half-ring average
amplitude and subtracting it from
in some way.
The way we do it is by taking, for a given event, a half-ring average
amplitude and subtracting it from 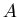 :
:
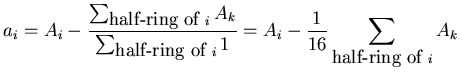 |
(77) |
then substituting the 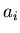 , rather than
, rather than 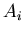 , into Eq. 6.23.
We take the half-ring where the channel belongs,
either right or left, depending on the field polarity,
rather than a full ring, because the calibrated amplitudes
of the two halves of the detector are quite different due to the additional
ionization from
, into Eq. 6.23.
We take the half-ring where the channel belongs,
either right or left, depending on the field polarity,
rather than a full ring, because the calibrated amplitudes
of the two halves of the detector are quite different due to the additional
ionization from 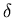 -electrons on one side.
One peculiar side effect, introduced by the subtraction, is an
auto-anticorrelation in the covariance matrix.
-electrons on one side.
One peculiar side effect, introduced by the subtraction, is an
auto-anticorrelation in the covariance matrix.
Figure 6.5:
Covariance matrix cov(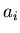 ,
,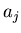 ) of the Si pad array in run 3192.
The color scale is logarithmic, units are
) of the Si pad array in run 3192.
The color scale is logarithmic, units are 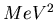 .
The matrix is symmetric.
Increased elements next to the main diagonal indicate
the adjacent neighbour cross-talk.
Non-uniform overall landscape is due to the beam offset and the
beam's geometrical profile.
The white diagonals represent the autocorrelation discussed in subsection
6.5.3.
The ``cross'' in the middle corresponds to dead channels.
.
The matrix is symmetric.
Increased elements next to the main diagonal indicate
the adjacent neighbour cross-talk.
Non-uniform overall landscape is due to the beam offset and the
beam's geometrical profile.
The white diagonals represent the autocorrelation discussed in subsection
6.5.3.
The ``cross'' in the middle corresponds to dead channels.
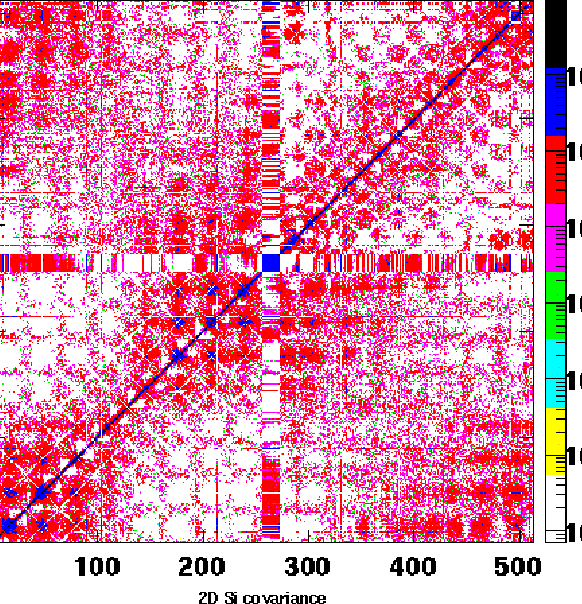 |
Namely, the channels of the same half-ring
(e.g., 1 and 32, 2 and 31, see subsection 6.5.2
for the channel numbering) appear anticorrelated.
This is seen on Fig. 6.5 as white diagonal lines.
The mechanism is simply the fact that when 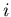 and
and 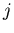 belong to the
same half-ring,
belong to the
same half-ring,
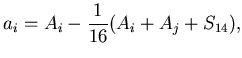 |
(78) |
where 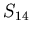 is an amplitude sum over 14 other channels of the same half-ring,
and
is an amplitude sum over 14 other channels of the same half-ring,
and
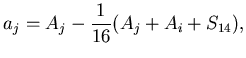 |
(79) |
then 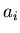 and
and 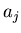 are anti-correlated no matter what the physical origins of
are anti-correlated no matter what the physical origins of 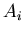 and
and 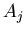 are.
Elimination of this anticorrelation requires subtracting a different
term (with
are.
Elimination of this anticorrelation requires subtracting a different
term (with 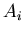 and
and 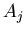 excluded) for every same half-ring
pair
excluded) for every same half-ring
pair 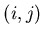 , which would complicate the computations enormously.
How large is the anticorrelation so induced ?
Based on the Eq. 6.25 and 6.26,
and using identities C.4 and C.5:
, which would complicate the computations enormously.
How large is the anticorrelation so induced ?
Based on the Eq. 6.25 and 6.26,
and using identities C.4 and C.5:
where
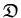 denotes variance.
If the leading cause of non-zero
cov
denotes variance.
If the leading cause of non-zero
cov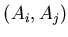 is the
common event multiplicity (which assumption
practically amounts to neglecting the
identity of the indices
is the
common event multiplicity (which assumption
practically amounts to neglecting the
identity of the indices 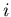 and
and 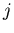 as long as
as long as 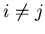
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif) ),
then a crude estimation can be done using
),
then a crude estimation can be done using
cov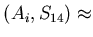 cov cov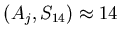 cov cov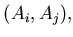 |
|
|
(81) |
![$\displaystyle {\mathfrak{D}}[S_{14}] \approx
14{\mathfrak{D}}[A_i]+14\times13$](img582.gif) cov cov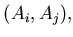 |
|
|
(82) |
and Eq. 6.27 can be rewritten entirely in terms of
a single channel variance
![$ {\mathfrak{D}}[A]$](img583.gif) and a two channel covariance
cov
and a two channel covariance
cov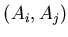 :
:
cov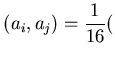 cov cov![$\displaystyle (A_i,A_j)-{\mathfrak{D}}[A]) \approx -\frac{1}{16}{\mathfrak{D}}[A],$](img585.gif) |
(83) |
where the last approximation is based on the practical
(and expected) observation that
 cov
cov![$ (A_i,A_j)\vert \ll {\mathfrak{D}}[A]$](img587.gif) .
The
.
The
![$ {\mathfrak{D}}[A]$](img583.gif) can be estimated based on an
can be estimated based on an  of a histogram
like the one shown on Fig. 6.1 (but including all channels)
and is approximately
of a histogram
like the one shown on Fig. 6.1 (but including all channels)
and is approximately
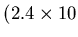 keV
keV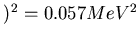 .
In other words, we expect to see a number of negative covariance elements
around
.
In other words, we expect to see a number of negative covariance elements
around
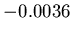 MeV
MeV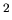 as one of the features of the matrix.
as one of the features of the matrix.




Next: Cross-talk evaluation: results and
Up: Cross-talk analysis
Previous: Channel wiring and numbering
Contents
Mikhail Kopytine
2001-08-09