Kopytine's homepage

$dN/d\eta$ matching: Si vs spectrometer

This subsection explains the core procedure of centrality determination. It consists in finding the number $c$ which gives the closest match between the Si and the spectrometer data, and is illustrated by the chart in Fig. 4.3.

Figure 4.3: Determination of the trigger centrality by matching the Si and spectrometer multiplicity data. The multiplicity comparison is done withing the same multiplicity classes based on T0 amplitude, see text.

In my method I scan correlation between the normalized (under some tentatively assumed trigger centrality) spectrometer $dN/d\eta$ of non-identified tracks and the Si $dN/d\eta$. Acceptance correction for the non-identified spectrometer tracks is described in subsection  4.1.4. The spectrometer $dN/d\eta$ is corrected for the inefficiencies due to dead channels, presence of the pad chamber in the trigger, tracking confidence level cuts, and includes extrapolation to $p_{T}=\infty$. The correlation is scanned varying the T0 multiplicity, with 14 fixed T0 thresholds. The centrality that makes spectrometer and Si $dN/d\eta$ match with the factors shown in the Table 4.3 is accepted. An example of such centrality fitting is illustrated by Fig.  4.4 and Fig.  4.5.

Figure: Left: correlation between $\,dN/\,d\eta$ obtained by charged track counting in the spectrometer and fired pad counting in the Si, found to be the best for a particular spectrometer setting. Right: positions of the multiplicity bins of the left plot along the ``diagonalized'' and normalized T0 amplitude.

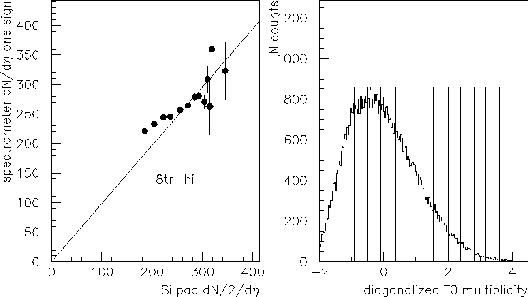Shown in the right part of Fig.  4.4 is the ``diagonalized'' T0 distribution from two PMT tubes on the $\delta$-free side. (The ``diagonalization'' means that distributions from two tubes on the $\delta$-free side were gainmatched, the covariance matrix that describes their correlation was diagonalized, and the value plotted is the diagonalized coordinate which is correlated with multiplicity. The zero of the normalized unit is chosen at the mean vealue of the distribution.) The points shown correspond to 14 centrality bins with boundaries 0, .0001, .0002, .0005, .001, .0025, .005, 0.01, 0.02, 0.04, 0.06, 0.08, 0.10, 0.12, 0.14, later referred to as $c_i$. Of course, the thresholds $t_i$ change with different values assigned as the overall trigger centrality. The vertical lines across the T0 distribution in the right panel of Fig.  4.4 show locations of the thresholds which maximize the correlation in the left panel.

Figure 4.5: $\chi ^2/NDF$ between actual correlations and the one expected on the basis of acceptance simulation, vs the number of points involved, for three different centralities.

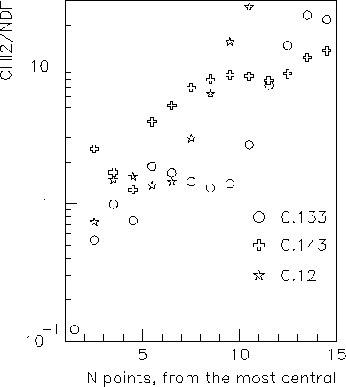Fig.  4.5 justifies why the correlation on Fig.  4.4 was found to be maximized by the centrality chosen. It shows the $\chi^2$ (per number of degrees of freedom) between each of three possible correlations and the one expected on the basis of acceptance simulation (see Table  4.3), vs the number of points involved. Data for three close choices of centrality are shown, the best choice is the one plotted by $\circ$.

The trend present on most figures like Fig.  4.4, left, (analyzed separately for every spectrometer setting) is a flattening of the correlation slope for lower multiplicity bins, as compared to a perfect correlation, especially for those bins where central T0 distribution deviates significantly from the valid beam one. The centrality thresholds are chosen based on the interpolation of the integrated T0 amplitude distribution $dN/dA$,

$$f(t) = \int^{\infty}_{t} \frac{\,dN}{\,dA} \,dA,$$

where $dN/dA$ is normalized so that $f(-\infty) = c$. Recall that these runs are central triggered. Normalization of every run period is done with $dN/dA$ of that period, i.e. the physics runs are normalized using their own $dN/dA$. The above mentioned 14 thresholds ${t}_{i}$ come from solving numerically the 14 equations

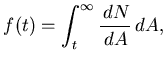
$$f({t}_{i}) = {c}_{i}.$$ (28)

From this it is clear that the bins to the left of the maximum in $dN/dA$ contain a broader composition of true centralities. However, the correlation in $dN/d\eta$ between the Si and the spectrometer holds as long as the tracks in the numerator of equation (4.16) come from events which are unbiased representatives of their centrality class. Recall here that both T0 and spectrometer, but not the Si, enter the trigger. Can we hope that the events in question are unbiased in this sense ? No, the bin contents to the left of the maximum in $dN/dA$ are the ones which deviate from the minimum bias T0 distribution the most ! Selection of these events is obviously the most affected by the trigger requirement of a spectrometer track. This explains why the correlation flattens out, i.e. the Si $dN/d\eta$ drops faster than the ``same'' quantity from the spectrometer.