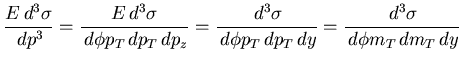Next: How to extract the
Up: Acceptance correction
Previous: Acceptance correction
Contents
Kopytine's homepage
The total energy 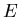 and a three-dimensional vector of momentum
and a three-dimensional vector of momentum 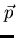 of
a particle, emitted in an interaction, along with that particle's
internal quantum numbers
(mass
of
a particle, emitted in an interaction, along with that particle's
internal quantum numbers
(mass 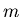 , charge, spin, strangeness, baryon number, etc),
carry important information about the dynamics of the
interaction.
The simplest way to analyze this information is by using statistical
distributions of particles with respect to various kinematical variables,
derived from its Minkowski energy-momentum four-vector
, charge, spin, strangeness, baryon number, etc),
carry important information about the dynamics of the
interaction.
The simplest way to analyze this information is by using statistical
distributions of particles with respect to various kinematical variables,
derived from its Minkowski energy-momentum four-vector
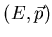 .
Among such variables are
.
Among such variables are
- transverse momentum
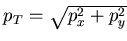 ,
,
- transverse energy
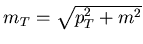 ,
,
- transverse kinetic energy
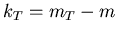 ,
,
- rapidity
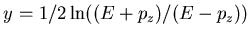 ,
,
- pseudorapidity
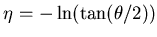 ,
where
,
where 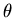 is zenith angle.
is zenith angle.
It is a popular practice to use 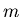 ,
, 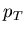 ,
, 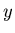 and azimuthal angle
and azimuthal angle 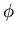 instead of (
instead of (
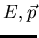 ), because in the former set of variables three
(
), because in the former set of variables three
(
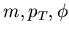 ) are Lorentz-invariant with respect to
translations along the
) are Lorentz-invariant with respect to
translations along the
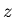 axis, whereas
axis, whereas 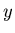 is Lorentz-transformed by a simple addition
of a number, so that
is Lorentz-transformed by a simple addition
of a number, so that 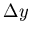 is Lorentz-invariant.
is Lorentz-invariant.
In particle physics, one uses the notion of
a differential cross-section of particle production
![[*]](file:/usr/local/lib/latex2html/icons/footnote.gif)
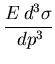 |
(3) |
With our preferred set of kinematical variables, one notices that
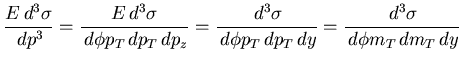 |
(4) |
Whatever reference is chosen to measure 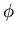 , in practice one will see
a set of interaction events averaged over all possible azimuthal orientations
of the colliding system, unless one's experiment is more sensitive to some
of them than to others.
For experiments which do not distinguish azimuthal orientations (like NA44),
nature performs a Monte-Carlo integration of Eq. 4.1 over
, in practice one will see
a set of interaction events averaged over all possible azimuthal orientations
of the colliding system, unless one's experiment is more sensitive to some
of them than to others.
For experiments which do not distinguish azimuthal orientations (like NA44),
nature performs a Monte-Carlo integration of Eq. 4.1 over
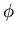 , and one is left with
, and one is left with
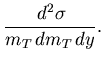 |
(5) |
It may be more direct to talk about
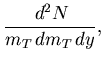 |
(6) |
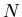 being the number of particles of given identity emitted in an interaction
event.
What one measures however is
being the number of particles of given identity emitted in an interaction
event.
What one measures however is
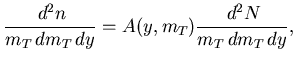 |
(7) |
where 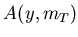 is an acceptance function.
is an acceptance function.
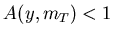 due to experimental inefficiencies.
Technically,
due to experimental inefficiencies.
Technically, 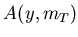 is represented in the analysis by a
TURTLE[40]-based Monte Carlo
simulation procedure and takes into account the effects of focusing
and analyzing optics of the spectrometer
as well as tracking efficiency and decays:
is represented in the analysis by a
TURTLE[40]-based Monte Carlo
simulation procedure and takes into account the effects of focusing
and analyzing optics of the spectrometer
as well as tracking efficiency and decays:
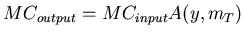 |
(8) |
The output from the single particle analysis will be presented in form
of 1D distributions, or integrals of Eq. 4.4:
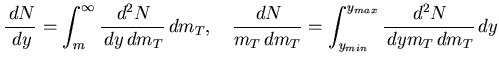 |
(9) |




Next: How to extract the
Up: Acceptance correction
Previous: Acceptance correction
Contents
Mikhail Kopytine
2001-08-09
![]() and a three-dimensional vector of momentum
and a three-dimensional vector of momentum ![]() of
a particle, emitted in an interaction, along with that particle's
internal quantum numbers
(mass
of
a particle, emitted in an interaction, along with that particle's
internal quantum numbers
(mass ![]() , charge, spin, strangeness, baryon number, etc),
carry important information about the dynamics of the
interaction.
The simplest way to analyze this information is by using statistical
distributions of particles with respect to various kinematical variables,
derived from its Minkowski energy-momentum four-vector
, charge, spin, strangeness, baryon number, etc),
carry important information about the dynamics of the
interaction.
The simplest way to analyze this information is by using statistical
distributions of particles with respect to various kinematical variables,
derived from its Minkowski energy-momentum four-vector
![]() .
Among such variables are
.
Among such variables are
![]()