c - Résolution en paramètre d'impact

Un autre aspect crucial de la reconstruction concerne la résolution en position de l'hélice. En effet, cette caractéristique est prédominante pour la localisation du vertex primaire ainsi que, comme nous l'aborderons ultérieurement, pour l'efficacité de reconstruction des vertex secondaires.

Pour tester cette résolution en position de la trace, nous utilisons le calcul de la distance de plus courte approche (dca), encore appelée ``paramètre d'impact''dans le vocabulaire de la physique des particules, des traces primaires au point de collision. Il est également intéressant de décomposer cette variable suivant ses composantes sur l'axe Z (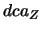$dca_{Z}$), l'axe Y (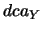$dca_{Y}$) et l'axe X (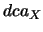$dca_{X}$). La figure 4.9 traduit l'évolution des trois projections de la distance de plus courte approche en fonction de l'impulsion transverse des particules primaires analysées. Les traces correspondantes sont correctement reconstruites.

Figure 4.9: Résolution en paramètre d'impact des particules primaires reconstruites.

Pour les traces comprenant les points de la TPC, du SSD et/ou du SVT, les trois variables étudiées ont un comportement similaire: la résolution en distance de plus courte approche au vertex primaire est supérieure à 1mm pour les traces de faible impulsion et atteint 200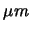$\mu m$ pour les particules très énergétiques. Pour ce même ensemble de traces avant association avec les points du détecteur de vertex, les distances de plus courte approche sont en moyenne cinq fois supérieures et ce, quelle que soit l'impulsion transverse dans l'intervalle considéré.

Nous pouvons faire deux remarques sur les conséquences de cette résolution en paramètre d'impact:

En ce qui concerne les particules primaires, l'erreur sur la distance de plus courte approche influe directement sur la résolution en position du vertex primaire. En effet, la résolution sur la position du point de collision est donnée par:

$$R\acute{e}solutionVertex_{i} = \frac{R\acute{e}solutionTrace_{i}}{\sqrt{N}}$$

où i est l'axe considéré et N le nombre de traces primaires mises en jeu pour déterminer la position du vertex primaire. Il est alors clair que l'on doit retrouver le facteur cinq entre la résolution en position des traces TPC seules et des traces TPC+SSD+SVT dans la précision de reconstruction du point de collision. Néanmoins, la procédure de reconstruction du vertex primaire réduit quelque peu cet écart en utilisant une méthode itérative. Une première estimation de la position du point de collision est réalisée et est alors intégrée dans le réajustement des paramètres des hélices. Les distances de plus courte approche donnent alors une nouvelle position du vertex primaire qui est à nouveau utilisée dans le réajustement des hélices. 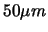Cette technique permet de limiter l'erreur sur la localisation du point de collision principal et les résultats obtenus sont de $200 \mu m$ en n'utilisant que la TPC et d'environ $50 \mu m$ en utilisant les trois détecteurs de trajectographie de la région centrale.

En ce qui concerne les traces secondaires, il n'est évidemment pas possible d'améliorer la résolution en position de ces traces en injectant la position du vertex primaire dans le réajustement des paramètres des hélices. Les erreurs en position resteront donc inchangées et le facteur cinq ne peut pas être réduit. Cette caractéristique est à l'origine de l'intégration du SVT mais également du SSD qui, comme nous l'avons démontré, accroît de façon importante le nombre de particules secondaires reconstruites.