



Next: b - La stabilité
Up: L'analyse des données brutes
Previous: L'analyse des données brutes
Nous symbolisons les données brutes par la notation 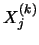 , correspondant à un événement k et une piste j. Le piédestal d'une piste, qui est la moyenne des valeurs brutes estimée sur N événements, est alors calculé de la façon suivante:
, correspondant à un événement k et une piste j. Le piédestal d'une piste, qui est la moyenne des valeurs brutes estimée sur N événements, est alors calculé de la façon suivante:
La figure 2.2 montre la distribution des données brutes d'une piste évaluée sur 2000 événements.
Figure 2.2:
Distribution des valeurs brutes du signal sur une piste donnée.
|
|
Cette distribution suit une loi gaussienne de dispersion 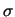 centrée sur le piédestal. L'erreur sur le piédestal est donnée par la relation:
centrée sur le piédestal. L'erreur sur le piédestal est donnée par la relation:
L'erreur relative du piédestal par rapport à la dispersion de sa distribution est de l'ordre de:
Pour atteindre une erreur relative de l'ordre de 1%, il est nécessaire d'estimer le piédestal sur environ 10000 événements.
Walter Pinganaud 11 Octobre 2000
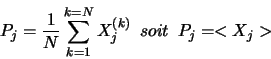
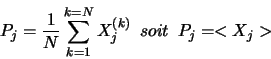
![]() centrée sur le piédestal. L'erreur sur le piédestal est donnée par la relation:
centrée sur le piédestal. L'erreur sur le piédestal est donnée par la relation: