a - Confrontation des mesures des corrélations entre les pistes voisines

avec les couplages déduits de l'étude du partage du signal

Ce couplage fort entre les pistes voisines des détecteurs Eurysis que nous observons sur le bruit, n'a pas été mis en évidence, lors de l'analyse des données prises sous faisceau, pour les signaux résultant du passage d'une particule. Néanmoins, les mécanismes de couplage du bruit et du signal physique sont très différents, le couplage observé sur le signal déposé par les particules à principalement lieu lors de la collection des charges sur les pistes implantées, le mouvement des nuages de charges (électrons ou trous) induisant des charges miroirs sur les pistes voisines.

Néanmoins, nous pouvons relever une certaine persistance des effets de corrélation observés sur le bruit même pour les données prises sous faisceau. Comme l'indique le tableau 2.1, le rapport des valeurs de signal sur bruit entre les faces P et N pour les détecteurs Canberra est de l'ordre de l'unité. Pour les détecteurs Eurysis, le rapport signal sur bruit est deux fois plus faible sur la face N que sur la face P.

Tableau 2.1: Valeurs du rapport signal sur bruit mesurées en faisceau pour les détecteurs Canberra et Eurysis.

Det. & FEE	Faisceau GeV/c	S/B Face P	S/B Face N
Canb. + ALICE 128	6	42	39
Eur. + ALICE 128	6	59	32

Nous avons utilisé le modèle simple développé auparavant en prenant en compte les couplages jusqu'à la n $^{i\grave{e}me}$ voisine. Un algorithme de minimisation permet alors d'extraire les coefficients de couplage en connaissant les valeurs des coefficients de corrélation (figure 2.20).

Figure 2.20: Distribution des coefficients de couplage et comparaison des coefficients de corrélation mesurés et de ceux déduits des coefficients de couplage pour un détecteur Eurysis face N.

En supposant que les signaux des pistes ont des dispersions similaires, et que ceux-ci sont totalement décorrélés avant influence mutuelle, nous pouvons exprimer le bruit d'une piste j donnée comme étant:

$$RMS_{j}(Apr\grave{e}s\ \ couplage) = RMS_{j} + \vert C_{k}\vert\sum^{k=N}_{k=1}{RMS_{j-k}+RMS_{j+k}}$$

soit

$$RMS_{j}(Apr\grave{e}s\ \ couplage) = RMS_{j}(1+ \sum^{k=N}_{k=1}\vert C_{k}\vert$$

En sommant sur les dix premiers coefficients de couplage qui seuls sont significatifs, nous obtenons:

$$RMS_{j}(Apr\grave{e}s\ \ couplage) = 1.2*RMS_{j}$$

Le bruit est donc systématiquement supérieur d'un facteur 1.2 sur la face N. De plus, dans l'hypothèse où toutes les dispersions du signal des pistes ne sont pas, comme dans notre situation, similaires, cet effet est encore renforcé. Nous observons sur le détecteur Eurysis testé un bruit de l'ordre 5 sur la face P et de 7 unités ADC sur la face N, cette dissymétrie est alors tout à fait compatible avec les coefficients de couplage mesurés.

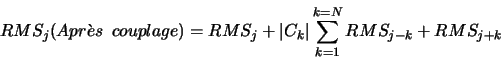
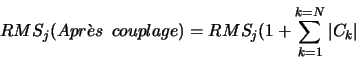
L'influence de ces coefficients de couplage semble donc produire un effet non négligeable, y compris pour l'étude de données collectées en présence de faisceau puisqu'il affecte sensiblement les valeurs du rapport signal sur bruit.

Notons également que la présence d'une piste très bruyante induit systématiquement une région très bruyante du fait de la forte corrélation de l'ordre de 20 à 30%.