d - Calcul de la position d'un cluster

La position reconstruite est déduite de la distribution du signal des pistes dans le cluster. Pour cela, nous utiliserons principalement deux méthodes:

Le centre de gravité:

C'est le barycentre des positions des pistes pondérées par le signal sur celles-ci:

$$position_{Cluster}=\frac{\sum_{i\in cluster}signal_{i}\times position_{i}}{\sum_{i\in cluster}signal_{i}}$$

C'est la méthode la plus naturelle mais elle suppose l'hypothèse suivante: si un point d'impact est situé entre deux pistes, le rapport du signal collecté par les deux pistes est proportionnel à la distance du point à l'une des deux pistes. Ce comportement linéaire du partage de charges sur les pistes en fonction de la position du point d'impact est la conséquence implicite de l'hypothèse suivante: si la distribution de la charge du nuage électronique, transversalement aux pistes, est de forme carré et que la largeur de ce profil de charge est supérieure au pas inter-piste, alors la position du point d'impact initial correspond au centre de gravité des pistes touchées tel que nous le définissons ici. Dans notre situation, les modules testés ont un pas de 95 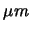$\mu m$ pour une dispersion du nuage électronique de l'ordre d'une dizaine de microns. Cet algorithme est donc mal adapté pour extraire la position du cluster. Néanmoins, pour les détecteurs de référence dont le pas de 50 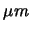$\mu m$ est réduit d'un facteur deux ou trois en fonction du nombre de pistes flottantes, cette hypothèse est quasiment vérifiée et une telle estimation de la position des clusters est raisonnable.

Eta:

L'algorithme 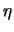$\eta$ [22], prend en compte la dépendance non linéaire de:

$$\eta=\frac{Signal_{droite}}{Signal_{droite}+Signal_{gauche}}$$

en fonction de la distance à la piste de gauche. Cette méthode correspond au raisonnement inverse suivi pour simuler le dépôt de charges sur les pistes. Elle est décrite en détail au chapitre 3 traitant de la simulation des modules du SSD.

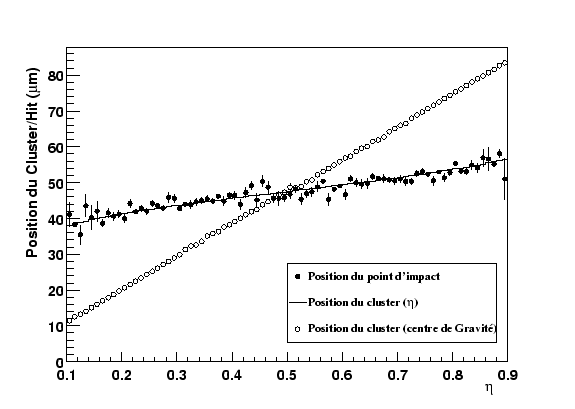
La figure 2.27 illustre les résultats obtenus avec les deux méthodes de reconstruction.

Figure 2.27: Comparaison des positions des clusters calculées par les méthodes du centre de gravité (cercles ouverts) et 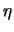$\eta$ (ligne pleine).

L'algorithme 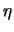$\eta$ donne une bonne approximation des coordonnées du point d'impact initial (cercles pleins). Le calcul de la position par l'évaluation du centre de gravité n'est qu'une estimation grossière dans le cas présent.

La stratégie de simulation exposée, il est impératif de vérifier le comportement global des simulations réalisées et de les confronter aux données collectées lors des tests sous faisceau.