a - Résolution à une trace

Nous nous focaliserons en premier lieu sur la résolution en position à ``une trace''. C'est en effet cette mesure qui justifiera l'approche choisie. Nous comparerons ensuite les résultats obtenus à ceux extraits des tests sous faisceau de pions. Il est important de juxtaposer ces deux approches car la seconde s'appuie d'une part, sur la reconstruction complète de l'événement, c'est-à-dire des trajectoires des pions et d'autre part, sur des événements de multiplicité unitaire. Avant de commenter les résolutions obtenues avec les simulations, il faut préciser que les événements analysés sont du même type que ceux pris lors des tests en multiplicité. Les clusters reconstruits peuvent donc se recouvrir et être séparés. Ces informations seront aussi utilisées pour estimer l'impact d'un recouvrement de deux clusters sur la résolution en position ainsi que pour quantifier la contribution de la séparation de deux clusters (lorsque cela est possible) à la dégradation de cette résolution.

Pour la suite de l'analyse, nous définissons la résolution à une trace comme l'écart-type moyen de l'erreur faite sur la position des clusters. L'erreur sur la position est directement mesurable car c'est la différence entre la position du point GEANT et la position calculée du cluster reconstruit. La résolution digitale du détecteur est la résolution à une trace du détecteur en associant la position du cluster à la position de la piste de plus fort signal dans celui-ci (piste centrale). La résolution digitale est principalement fonction du pas inter-piste du détecteur et du bruit des pistes. Dans le cas favorable où le bruit est négligeable,

$$Resolution_{DIGITALE} = \frac{Pas}{\sqrt{12}}$$

Dans notre cas, les détecteurs ont un pas de $95\mu m$ et donc, une résolution digitale de $27.4\mu m$.

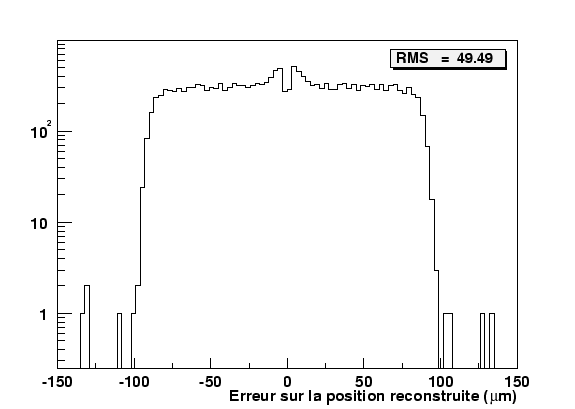
La figure 2.31 représente la résolution à une trace des clusters constitués d'une seule piste. La résolution expérimentale est de $24.1 \mu m$ ce qui indique que notre détecteur simulé n'a évidemment pas une résolution digitale sur toute la largeur du pas mais contient également une zone de partage de charges. Les points d'impact situés juste entre deux pistes ne généreront qu'improbablement une seule piste touchée, ceci réduisant la résolution digitale. Nous pouvons néanmoins estimer la largeur de la région où la charge n'est pas distribuée sur plusieurs pistes. La ``région digitale'' est égale à $Resolution_{1-piste}*\sqrt{12}$ soit $REGION_{DIGITALE}=24.1*\sqrt{12} = 83.5\mu m$. Cette région est inférieure au pas inter-pistes du détecteur, ce qui indique la présence d'une zone de partage du signal entre les pistes.

Figure 2.31: Distribution de l'erreur en position pour les clusters à une piste.

Le cas idéal en terme de résolution en position se présente lorsque le signal se partage sur plusieurs pistes. Comme illustré par la figure 2.32, l'erreur induite sur la position s'en trouve très largement réduite puisque l'écart-type de celle-ci n'est alors que de $12.8\mu m$ pour des clusters à deux pistes.

Figure 2.32: Distribution de l'erreur en position pour les clusters à deux pistes, non recouverts.

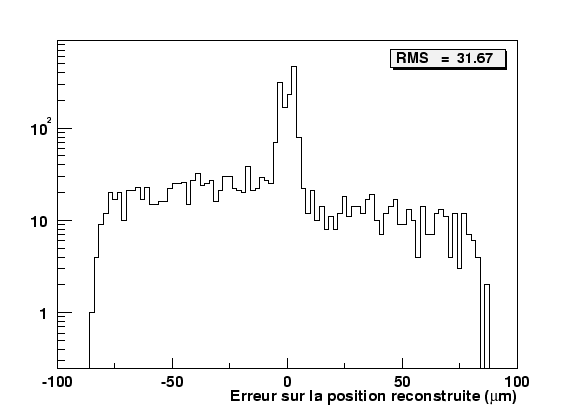
La figure 2.33 représente la distribution de l'erreur entre la position réelle du point d'impact et sa position calculée lorsque plusieurs clusters se recouvrent et sont résolus. Dans cette situation, la résolution est de $31.7\mu m$ et est directement comparable à celle de la figure 2.32 puisqu'il s'agit également de clusters à deux pistes.

Figure 2.33: Distribution de l'erreur en position pour les clusters à deux pistes, recouverts puis séparés.

Cette incertitude sur la position est uniquement due à la méthode de séparation des clusters: lorsque deux clusters se recouvrent, on cherche un trou dans le profil en signal des pistes. La piste qui a le signal le plus faible est alors partagée entre les deux clusters, chacun récupérant 50% du signal. La division systématique du signal en deux entraîne donc une incertitude sur la position que nous pouvons estimer. Si les deux contributions à la résolution sont indépendantes, elles s'ajoutent quadratiquement: $Resolution^2 = Resolution_{2Traces}^2 +Resolution_{S\acute{e}paration}^2$ soit $Resolution_{S\acute{e}paration} = \sqrt{31.7^2 - 12.8^2} = 29 \mu m$. La dégradation de la résolution en position pour les clusters séparés est de l'ordre de $29 \mu m$, ce qui peut paraître important. Cependant il faut apporter deux précisions:

Tout d'abord, c'est une limite supérieure qui peut être réduite en utilisant les informations contenues sur l'autre face du détecteur, comme on l'a vu précédemment, afin de partager le signal de manière plus judicieuse.

Outre l'avantage d'être parvenu à résoudre les deux clusters, pour les étapes suivantes de la reconstruction des traces, la résolution pour les clusters non séparés de deux pistes est de l'ordre de $49.5\mu m$(figure 2.34). Ceci conduit à une contribution du recouvrement de $47.8\mu m$.

Figure 2.34: Distribution de l'erreur en position pour les clusters à deux pistes, recouverts et non séparés.

Ces résultats sont tout à fait compatibles avec ceux obtenus en reconstruisant les traces des particules [23] dans le télescope où la résolution du détecteur Eurysis face N est de $22\mu m$. Pour nous placer dans les mêmes conditions, il faut rejeter tous les clusters recouverts, séparés ou non car les tests ont été effectués avec une particule par événement afin d'éviter toute ambiguïté. Dans ce cas, les simulations donnent une résolution de $23.3\mu m$. L'écart d'un micron qui n'est pas forcément significatif peut être attribué à plusieurs causes, la plus importante étant la proportion du nombre de clusters à deux pistes par rapport aux clusters à une piste (comme nous l'avons montré, la résolution est bien meilleure pour les clusters à deux pistes). On peut également incriminer la qualité du détecteur: le pourcentage de pistes mortes influe sur cette perte de résolution en ne permettant que la reconstruction partielle des clusters et induit donc une perte d'information sur la position. Le fait d'ajouter les clusters séparés ne dégrade que légèrement la résolution puisqu'ils ne représentent que 2% des cas, conduisant alors à une erreur moyenne de $23.5\mu m$.