b - Efficacité de construction des clusters dans un environnement dense

Pour évaluer la résolution à deux traces, deux méthodes peuvent être envisagées:

L'une consiste à reconstruire l'ensemble des traces des particules à partir des points d'impact laissés dans les différents plans de référence du télescope. Cette méthode est utilisée pour évaluer la résolution à une trace des détecteurs pour les mesures sans la cible de plomb. Les points d'impact dans le détecteur testé correspondent alors à l'intersection des traces reconstruites avec le plan du détecteur. A chaque point d'impact, on associe le cluster reconstruit le plus proche. Nous pouvons alors estimer la résolution à deux traces en considérant toutes les paires de points d'impact et en vérifiant pour chacune, si elle est associée à un ou deux clusters distincts. C'est la méthode la plus intuitive mais elle a l'inconvénient d'induire des biais importants dans l'analyse:

• La reconstruction des traces dans un environnement de haute multiplicité n'est pas facilitée par le faible angle d'ouverture du cône dans lequel se développe la gerbe électromagnétique, et par voie de conséquence la forte densité locale de clusters dans les détecteurs. Cette caractéristique est d'autant plus vraie que les détecteurs étudiés sont près de la cible.
• Un autre point négatif se traduit par la distribution en énergie des électrons (et positrons) secondaires. Ces énergies peuvent être faibles, de l'ordre de quelques GeV, et par conséquent, la diffusion dans le silicium n'est plus négligeable ce qui entraîne au mieux une mauvaise résolution en position pour ces traces. Ceci induit des ambiguïtés difficilement quantifiables dans l'association entre les points d'impact et les clusters.

Néanmoins, une étude précise peut être menée en utilisant la modélisation complète du détecteur. S'étant assuré de l'adéquation entre la simulation et les données, nous allons utiliser cette modélisation pour tester les algorithmes de clusterisation (et les différentes tentatives de résolution de clusters se recouvrant) et extraire une efficacité de séparation des paires de clusters en fonction de la distance entre les deux points d'impact qui les ont générés.

Il est maintenant important de définir ce que nous entendons par résolution à deux traces. Habituellement, elle représente la ``Distance en dessous de laquelle deux clusters ne peuvent être résolus''. Cette définition a l'avantage d'être simple mais n'est pas envisageable dans cette étude pour deux raisons:

La séparabilité de deux clusters ne dépend pas uniquement de la distance qui les sépare, mais également de l'endroit du détecteur où ils sont localisés. Sur la figure 2.35, deux exemples sont illustrés: les points d'impact sont également espacés mais il apparaît que dans la situation A où il y a peu de partage de charges, les clusters ne pourront être résolus. Inversement, dans l'exemple B, le partage de charges est réalisé, ce qui rend possible une éventuelle séparation des deux clusters.

Figure 2.35: Séparabilité des clusters pour deux localisations différentes.

De plus, la présence de bruit sur les pistes, ainsi que son inhomogénéité rend cette limite incertaine. L'extension spatiale des clusters rend également cette définition mal adaptée.

Il est également possible de définir la résolution à deux traces comme étant ``la distance au dessus de laquelle tous les clusters sont résolus''. Pour les mêmes arguments que précédemment, cette définition n'est pas satisfaisante. On ne peut pas définir de limite franche pour la résolution à deux traces. Il est alors plus indiqué de représenter l'efficacité de résolution de deux clusters en fonction de leur distance relative ce qui est une observable plus robuste.

Figure 2.36: Efficacité de résolution de deux clusters en fonction de leur distance relative.

La figure 2.36 représente cette efficacité pour plusieurs cas: on ne considère en premier lieu que les événements à deux traces.

En appliquant un algorithme de séparation des clusters (triangles), nous constatons que l'on parvient à résoudre les clusters jusqu'à une limite minimale d'environ $105 \mu m$, ce qui correspond aux cas favorables illustrés par le schéma 2.35 (cas B). Cette valeur correspond à la somme du pas et de la zone de partage. Les deux points d'impact tombent tous les deux dans une zone de partage de charges mais de façon à ce que pour le cluster de gauche, la piste de gauche soit favorisée lors de la collection des charges et inversement pour le cluster de droite. La limite supérieure au-delà de laquelle la majorité des clusters sont résolus se situe aux environs de $200 \mu m$. Cette distance induit dans tous les cas de figure, même les plus défavorables, un trou dans les profils en signal des pistes.

Si aucune tentative n'est faite pour séparer les clusters (croix), on peut faire plusieurs observations. La distance relative minimale entre les deux points d'impact est alors de $120 \mu m$, soit le cas favorable où les deux points sont situés dans la zone digitale (ou bien en bordure de la zone de partage), séparés par deux zones de partage et une zone digitale. De la même façon, tous les clusters sont reconstruits au-delà de trois pas car il y a toujours une piste non touchée entre les clusters.

On remarque également que le fait de séparer les clusters lorsque cela est possible conduit à une augmentation de l'efficacité de résolution de l'ordre de 20% sur la plage où il peut y avoir recouvrement.

Dans un environnement dense (cercles), comme c'est le cas dans les données, d'autres effets viennent biaiser les précédentes observations. Deux clusters, qui devraient être séparés s'ils étaient seuls, peuvent ne pas l'être dans le cas où un troisième est intercalé. Cette probabilité augmente avec leur distance relative. C'est effectivement ce qui est observé: la limite inférieure de résolution est conservée, mais plus la distance relative entre les deux clusters s'accroît, plus l'efficacité de résolution s'éloigne d'un comportement normal pour n'atteindre son maximum que vers $400 \mu m$.

Ces résultats soulèvent plusieurs questions auxquelles nous allons répondre:

i)

Comment évolue l'efficacité de reconstruction des clusters avec la densité
de points d'impact?

Figure 2.37: Efficacité de reconstruction en fonction de la densité de points d'impact et de la coupure pour des densités uniformes.

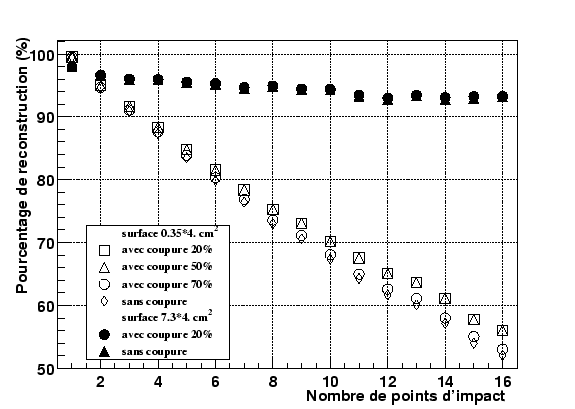
Sur la figure 2.37, nous avons représenté les pourcentages de clusters reconstruits en fonction de la densité de points d'impact dans le détecteur.

Intéressons-nous tout d'abord aux symboles pleins. Ils correspondent à l'efficacité de reconstruction des clusters pour une densité de points uniforme dans tout le détecteur. Cette efficacité est rapportée au nombre d'impacts trouvables dans le détecteur, ce qui signifie que les points localisés dans les zones mortes ne sont pas considérés (c'est-à-dire dans notre cas la puce morte, les autres pistes inactives n'étant pas déduites). Dans ces conditions, l'efficacité est supérieure à 93% pour un nombre de points d'impact inférieur à 16. Cette densité est déjà importante comparativement à la multiplicité attendue au RHIC pour les collisions centrales Au+Au (6 à 9 clusters par détecteur). On peut d'ores et déjà affirmer que la densité de points n'est pas un obstacle majeur pour STAR.

Il faut atteindre des densités très importantes pour voir cette efficacité chuter de façon significative, ce qui est illustré sur les courbes en symboles ouverts. Le rapport des surfaces touchées pour les deux ensembles de courbes est égal à $\frac{7.3*5}{6*0.35} = 17.4$. Une puce sur les six étant inactive, lorsque les impacts sont repartis sur toute la surface du détecteur, seuls $\frac{5}{6}$ des pistes du détecteur peuvent collecter du signal. Les courbes en symboles ouverts peuvent donc être comparées aux précédentes en multipliant le nombre de points d'impact par un facteur 17.4. Pour que l'efficacité s'effondre à une valeur de 80%, il faut atteindre dans le détecteur une densité uniforme de $17.4*6 = 104$ points. On remarquera également que les courbes d'efficacité varient bien linéairement avec le nombre de points d'impact.

ii)

Comment évolue l'efficacité de reconstruction des clusters avec la coupure en signal
permettant de reconnaître les trous?

Sur les courbes en symboles ouverts de la figure 2.37, nous avons fait varier la coupure en signal ( $coupure_{trou}$) entre 0, 20, 50 et 70% du signal. La densité est ici uniforme sur une fenêtre de 3.5mm correspondant à environ 36 pistes.

On observe premièrement que l'efficacité ne varie que très peu avec la coupure choisie: on peut accroître l'efficacité tout au plus de 4% en variant la coupure de 20% à aucune. Cette caractéristique a deux origines: d'une part, pour séparer deux clusters recouverts, il faut systématiquement que l'un d'eux donne lieu à un partage de charges sur plusieurs pistes. Cette probabilité est relativement faible car la zone de partage est de l'ordre d'une dizaine de microns pour un pas de 95 $\mu m$. Ceci explique la chute d'efficacité indépendamment de la coupure.

On peut également mentionner que la coupure en signal sur bruit minimale pour qu'une piste soit inclue dans un cluster est assez haute (de l'ordre de 3 à 5). Ceci a pour conséquence de résoudre implicitement les clusters reliés par une piste au signal sur bruit faible. C'est ce que l'on observe pour les courbes d'efficacité à 20 ou 50% qui sont très proches. La coupure en signal sur bruit induit une coupure permettant de repérer les trous correspondant à au moins 50%.

iii)

Comment évaluer la densité des points d'impact dans les simulations ou
les données?

Pour cela, comparons l'efficacité de reconstruction des clusters dans le cas d'une distribution uniforme des particules, mais sur une surface réduite, avec la distribution des clusters issue de GEANT. C'est ce qui est illustré par la figure 2.38: les triangles noirs correspondent à l'efficacité de reconstruction des clusters pour une surface de $0.35*4 cm^2$ et une distribution uniforme.

Figure 2.38: Efficacité de reconstruction en fonction de l'uniformité de la densité.

Les symboles ouverts correspondent à la densité donnée par GEANT sur l'ensemble du détecteur. Les clusters sont reconstruits avec ou sans coupure.

Un aspect de ces résultats peut choquer: l'évolution de l'efficacité en fonction du nombre de points d'impact n'est plus linéaire. En effet, les positions correspondant aux paires $e^+ e^-$ sont très corrélées comme on peut le voir pour les nombres de points 2 et 3: l'efficacité à 3 points est de l'ordre 79% alors que l'on pourrait s'attendre à 88%. Or, deux points correspondent la plupart du temps à l'électron primaire et à une paire où l'une des particules a disparu (recombinaison du positron ou bien diffusion d'une des deux particules hors du télescope). Les deux particules restantes sont peu corrélées et donc relativement faciles à reconstruire. Au contraire, les événements à 3 points sont constitués d'une paire et de l'électron primaire. Les points de la paire étant très proches en position, les clusters associés se recouvrent souvent ce qui explique la perte en efficacité de reconstruction. Pour expliquer le comportement des événements à 3 et 4 points, l'argument est le même: supposons que l'on ne puisse jamais résoudre les paires. La probabilité de reconstruction de ces événements est alors de $\frac{2}{3}=66.7\%$. Les événements à 4 points sont constitués d'une paire, de l'électron primaire et de l'une des particules d'une autre paire, ce qui donne une efficacité de $\frac{3}{4}=75\%$. La reconstruction est donc meilleure pour les événements à 4 points qu'à 3. Des considérations de densité atténuent cependant cette différence. Nous pouvons justifier la non linéarité de la courbe d'efficacité, par l'extension spatiale de la gerbe ou encore son angle d'ouverture qui tend à augmenter avec le nombre de points d'impact. Ceci explique le phénomène de saturation qui apparaît quand des grands nombres de points d'impact sont considérés.

Ces observations impliquent que la densité des points d'impact ou encore la surface touchée par la gerbe sont difficiles à extraire. Cependant, une surface correspondant à une dimension transverse aux pistes de 3.5mm semble être une bonne estimation.