L'association face à face des clusters - SCM

Avant de décrire les techniques employées pour réaliser l'association des clusters face à face, il est nécessaire de définir quelques notions de base:

L'association sur critère géométrique

:
Le premier des critères d'association des clusters que nous utilisons est un critère géométrique. Partons tout d'abord sur l'hypothèse simple que les clusters ne comportent qu'une piste et ont alors des positions entières correspondant à la position de la piste. Deux clusters peuvent être associés et donc donner naissance à un point d'impact reconstruit si et seulement si les pistes relatives à chacune des faces se croisent effectivement dans la zone active du détecteur. Soit une piste de la face P d'indice $I_{P}$, calculons le nombre de pistes qu'elle croise sur la face N.

Figure 3.16: Association géométrique.

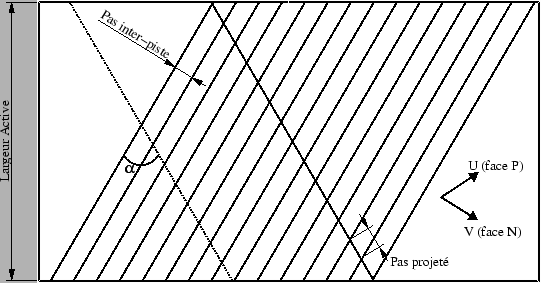
D'après la figure 3.16, la longueur d'une piste est égale à

$$l= \frac{Largeur_{Active}}{cos(\frac{\alpha}{2})}$$

avec $Largeur_{Active}$ la largeur de la zone active du détecteur et $\alpha$ l'angle stéréo entre les pistes des deux faces. Le pas des pistes de l'autre face projeté sur cette piste est égal à

$$Pas_{Proj}= \frac{Pas}{sin(\alpha)} = \frac{Pas}{2cos(\frac{\alpha}{2})sin(\frac{\alpha}{2})}$$

Le nombre de pistes croisant une piste sur la face opposée est donc

$$Trunc(\frac{l}{Pas_{Proj}}+1) = 15$$

où $Trunc()$ symbolise la fonction de troncature entière. Une piste de la face P croise 15 pistes sur la face N et deux pistes sur des faces opposées mais de même indice se coupent au milieu du détecteur. Pour qu'une piste d'indice $I_{N}$ soit associable avec $I_{P}$, il faut alors que la relation suivante soit vérifiée : $\vert I_{P}-I_{N}\vert\le 7$. Ce raisonnement reste valide pour les clusters à plusieurs pistes, et il suffit de remplacer l'index des pistes par les positions calculées des clusters. Ce seul critère géométrique suffit dans la grande majorité des cas à reconstruire les points d'impact. Il arrive cependant que des situations ambiguës se présentent.

L'ambiguïté

:
Nous entendons par ambiguïté, les configurations où la disposition des clusters ne permet pas une association bijective des clusters entre les faces opposées.

Figure 3.17: Exemple de situation ambiguë.

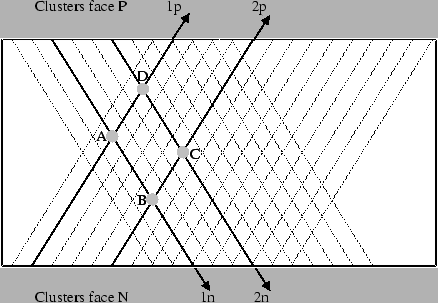
La figure 3.17 représente une telle configuration où deux points d'impact ont généré deux clusters sur chaque face. Néanmoins, des considérations uniquement géométriques ne suffisent pas pour décider si les points d'impact à reconstruire correspondent à la combinaison A-C ou bien B-D. Géométriquement, ces deux combinaisons ont la même probabilité d'être vraies. Il existe cependant une information supplémentaire qui peut être utilisée, sinon pour trancher, pour pondérer les probabilités d'existence des deux combinaisons: c'est l'information sur la perte d'énergie.

L'association par comparaison des pertes d'énergie

:
Le principe de base de cette méthode d'association de clusters exploite la corrélation entre les charges déposées par une particule sur les deux faces d'un détecteur ($S_{ADC}^{P}$ et $S_{ADC}^N$). Il s'agit ensuite de construire la distribution $S_{ADC}^{P} = f(S_{ADC}^N)$ pour les clusters non ambigus. Il est possible d'extraire de la distribution précédente la droite de corrélation parfaite par une méthode de minimisation. En construisant alors la distribution $S_{ADC}^P-f(S_{ADC}^N)$ nous pouvons accéder aux deux grandeurs $\sigma_{corr}$ et $moy_{corr}$ qui caractérisent la dispersion de la corrélation des couples de clusters autour de la droite de corrélation parfaite.

Figure 3.18: Corrélation des charges collectées sur les deux faces du détecteur.

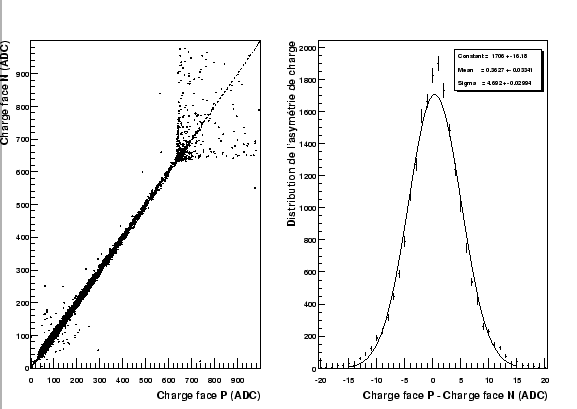
La figure 3.18 montre la corrélation de charge entre les clusters issus du même point d'impact (à gauche). La perte de linéarité pour les grands nombre de coups ADC est due à la saturation des signaux sur au moins l'une des faces. Sur le graphe de droite est représentée la distribution $S_{ADC}^P-f(S_{ADC}^N)$.

Comme cette distribution est de forme gaussienne, il est justifié d'affecter à chaque couple de clusters un poids proportionnel à

$$p = GAUSS(S_{ADC}^P-f(S_{ADC}^N) , \sigma_{corr} , moy_{corr})$$

où $GAUSS(x,\sigma,m)$ est la valeur au point x d'une gaussienne d'écart-type $\sigma$ et de moyenne $m$. Dans le cas illustré par le schéma 3.17, nous pouvons alors affecter à chacune des deux combinaisons une probabilité :

$$Prob(A,C) = \frac{p(A)p(C)}{p(A)p(C)+p(B)p(D)}$$

où $p(I)$ est le poids du point $I$ et $Prob(I,J)$ la probabilité (normalisée) de l'existence de la combinaison des points I-J. Nous avons maintenant associé une probabilité à chaque configuration. Cependant il est important pour la suite de l'analyse de caractériser les points d'impact reconstruits. Les probabilités des configurations étant normalisées, il est alors justifié d'associer à chaque point, la somme des probabilités des combinaisons dans lesquelles il apparaît. Ce poids ainsi défini correspond à la probabilité d'existence du point sur l'ensemble des configurations possibles. Dans notre cas simple, ce poids devient $Prob(A) = Prob(A,C)$. La difficulté de résolution des situations ambiguës provient de la multiplicité des configurations possibles. Il est alors nécessaire de caractériser les situations pour pouvoir les traiter correctement, ceci fera l'objet du dernier point que nous allons aborder.

Le groupement de clusters ambigus

:
Pour pouvoir résoudre ou pondérer les ensembles de clusters ambigus, il faut pouvoir les repérer. La méthode systématique utilisée est la suivante:

Les clusters sont d'abord ordonnés suivant leur position sur chacune des faces. Puis, nous tentons d'associer géométriquement le premier cluster de la face P (1p) avec tous les clusters de la face N (In). Si le cluster suivant de la face P (2p) peut être associé avec au moins un des clusters précédemment associé à 1p, il est ajouté au groupement courant ainsi que tous les clusters de la face N qui lui sont associés géométriquement. Puis le cluster 3p est à son tour testé. Lorsque la condition cesse d'être vraie, le groupement est complet et un nouvel ensemble de clusters ambigus est recherché.

Ces groupements sont symbolisés par la notation suivante: 1pInJnKn...2pLnMn... où In, Jn, Kn, ... sont les clusters de la face N associés avec le cluster 1p, et Ln, Mn, ... ceux associés avec le cluster 2p. L'intersection des ensembles (In, Jn, Kn, ...) et (Ln, Mn, ...) n'est pas vide. La situation de la figure 3.17 peut donc être symbolisée par 1p1n2n2p1n2n.

Les différentes situations sont traitées individuellement y compris jusqu'aux configurations où les groupements contiennent trois clusters ambigus sur chaque face.

Nous n'allons pas, dans cette partie, examiner toutes les différentes configurations de groupements de clusters ambigus [26].

Etudions à présent les résultats obtenus par le module de reconstruction et celui d'association.