![\includegraphics[width=0.8\linewidth,height=7cm]{/home/suire/these/xfigure/Ssd/gap.eps}](img158.gif)
| |||||||||||||||
L'intérêt d'utiliser un détecteur constitué d'un matériau dense réside dans le fait que le nombre d'atomes par unité de volume étant grand, le pouvoir d'arrêt est élevé et l'épaisseur peut être réduite. La détection du passage d'une particule dans le détecteur est alors obtenue en appliquant au matériau qui le constitue un champ électrique externe afin de collecter les électrons libres produits par le passage de la particule à détecter. Ce matériau ne peut donc être isolant. Ce ne peut non plus être un conducteur car les fluctuations du courant produit par les charges libres seraient très supérieures à l'impulsion à détecter. La solution est fournie par les semi-conducteurs dont nous allons brièvement rappeler les propriétés.
Les états quantiques des électrons dans les solides ordonnés (cristaux) sont caractérisés par l'apparition de bandes continues d'énergie séparées par des bandes d'énergie interdite (gap). On distingue en particulier les bandes de valence dans lesquelles les électrons sont liés à des atomes ou molécules du réseau, et les bandes de conduction dans lesquelles les électrons sont libres de se déplacer dans le volume total du cristal. En fait, n'interviennent pour les phénomènes de conduction que la bande de valence de plus haute énergie et la bande de conduction d'énergie la plus basse, voir Fig. 3.1.
![\includegraphics[width=0.8\linewidth,height=7cm]{/home/suire/these/xfigure/Ssd/gap.eps}](img158.gif)
| |||||||||||||||
La position relative et le degré de remplissage de ces deux bandes d'énergie définissent les propriétés de conductibilité électrique du matériau. Un isolant est un matériau dont le gap entre les deux bandes est élevé (E![]()
![]() 5 eV), un semi-conducteur possède en revanche un gap nettement plus faible (E
5 eV), un semi-conducteur possède en revanche un gap nettement plus faible (E![]()
![]() 1 eV). Dans le cas d'un métal, le gap est nul ou, autrement dit, la dernière bande occupée n'est pas pleine. Donc même à très basse température, des électrons sont libres de se déplacer dans l'ensemble du réseau du cristal, voir tableau 3.1.
1 eV). Dans le cas d'un métal, le gap est nul ou, autrement dit, la dernière bande occupée n'est pas pleine. Donc même à très basse température, des électrons sont libres de se déplacer dans l'ensemble du réseau du cristal, voir tableau 3.1.
A 0![]() K, les semi-conducteurs ont ainsi une conductivité nulle puisque tous les électrons sont bloqués dans la bande de valence. A température non nulle un équilibre s'établit entre les électrons et les phonons du réseau. Cet équilibre est évidemment un équilibre dynamique entre le processus d'excitation des électrons vers la bande de conduction et le processus inverse. Lorsqu'un électron passe de la bande de valence à la bande de conduction, il laisse derrière lui, en un site particulier du réseau, une charge positive que l'on désigne sous le nom de trou. A l'équilibre le nombre d'électrons dans la bande de valence est égal au nombre de trous du réseau. Les électrons ainsi libérés, soumis à un champ électrique, peuvent se déplacer et induire un courant détectable. De la même façon un trou créé sur un atome du réseau peut être comblé par un électron d'un atome voisin qui va donc être ionisé. De proche en proche, une charge positive peut ainsi se déplacer. On désigne sous le nom générique de porteurs libres les trous et les électrons susceptibles de créer un courant de charges sous l'action d'un champ électrique.
K, les semi-conducteurs ont ainsi une conductivité nulle puisque tous les électrons sont bloqués dans la bande de valence. A température non nulle un équilibre s'établit entre les électrons et les phonons du réseau. Cet équilibre est évidemment un équilibre dynamique entre le processus d'excitation des électrons vers la bande de conduction et le processus inverse. Lorsqu'un électron passe de la bande de valence à la bande de conduction, il laisse derrière lui, en un site particulier du réseau, une charge positive que l'on désigne sous le nom de trou. A l'équilibre le nombre d'électrons dans la bande de valence est égal au nombre de trous du réseau. Les électrons ainsi libérés, soumis à un champ électrique, peuvent se déplacer et induire un courant détectable. De la même façon un trou créé sur un atome du réseau peut être comblé par un électron d'un atome voisin qui va donc être ionisé. De proche en proche, une charge positive peut ainsi se déplacer. On désigne sous le nom générique de porteurs libres les trous et les électrons susceptibles de créer un courant de charges sous l'action d'un champ électrique.
Dans un cristal de silicium à 310![]() K, nous avons les caractéristiques suivantes:
K, nous avons les caractéristiques suivantes:
![\begin{figure}
\centering\includegraphics[width=14cm,height=12cm,clip=true,draft=false]
{/home/suire/these/xfigure/Ssd/dopage.eps} \end{figure}](img166.gif) |
Ces électrons supplémentaires lorsqu'ils sont ionisés créent des trous sur chaque atome de dopant. Cependant, ces trous ne sont pas capable de se déplacer à la différence des trous intrinsèques. Pour cela, il faudrait faire passer un électron de la valence vers l'état d'énergie de l'électron libre du dopant et donc fournir une énergie de l'ordre de E![]() .
Le dopage a donc deux effets :
.
Le dopage a donc deux effets :
Un raisonnement similaire s'applique pour le dopage au moyen d'un atome trivalent. Dans ce cas, un niveau accepteur est introduit juste au-dessus du niveau supérieur de la bande de valence. Dans le réseau ainsi réalisé, la conduction se fait majoritairement par les trous, i.e. un électron de la valence passe dans le niveau accepteur et crée un trou dans la bande de valence qui est libre se propager de proche en proche.
Nous obtenons ainsi trois types de semi-conducteurs, les semi-conducteurs intrinsèques notés i, les semi-conducteurs de type n et p, suivant que leur conduction est dominée par les électrons ou les trous3.2. La conductivité des semi-conducteurs dopés est très supérieure à celle des semi-conducteurs intrinsèques. L'utilisation d'un matériau de ce type comme détecteur de particules ne pourra être réalisé que si l'on réussit à construire un assemblage dont la conductivité est très notablement diminuée. La solution à ce problème est contenue dans la jonction p-n.
Considérons un cristal de type n, ayant une concentration N![]() d'atomes donneurs dans lequel on fait diffuser sur une face une concentration N
d'atomes donneurs dans lequel on fait diffuser sur une face une concentration N![]() d'atomes accepteurs. Dans cette zone, N
d'atomes accepteurs. Dans cette zone, N![]()
![]() N
N![]() , la conduction est assurée par les trous largement excédentaires, qui vont diffuser dans la région n, en laissant l'atome accepteur dont ils proviennent dans un état de charge négatif. De la même façon, les électrons libres de la région de type n, vont diffuser vers la région de type p en laissant les atomes donneurs dans un état de charge positif.
, la conduction est assurée par les trous largement excédentaires, qui vont diffuser dans la région n, en laissant l'atome accepteur dont ils proviennent dans un état de charge négatif. De la même façon, les électrons libres de la région de type n, vont diffuser vers la région de type p en laissant les atomes donneurs dans un état de charge positif.
La zone de contact n-p ne contient plus de charge mobiles, elle est dite désertée. De plus, la présence d'atomes accepteurs et donneurs ionisés de part et d'autre de la zone de contact crée une zone de charge d'espace, et ainsi un champ électrique qui s'oppose au déplacement ultérieur de charges supplémentaires. Cette situation est résumée sur la figure 3.3.
A l'équilibre, le champ se fixe à une valeur qui annule la diffusion des trous et des électrons. La mécanique statistique impose alors que les niveaux de Fermi (plus exactement les potentiels chimiques au niveau de Fermi) des deux zones soient identiques. Comme ces niveaux sont l'un voisin de E![]() (type p) et l'autre voisin de E
(type p) et l'autre voisin de E![]() (type n), c'est donc une énergie de l'ordre de E
(type n), c'est donc une énergie de l'ordre de E![]() (
(![]() 1 eV) que le potentiel créé doit compenser. Ce potentiel est ainsi de l'ordre du volt, et la taille de la zone désertée est de quelques microns.
1 eV) que le potentiel créé doit compenser. Ce potentiel est ainsi de l'ordre du volt, et la taille de la zone désertée est de quelques microns.
La structure simple qui constitue la jonction p-n pourrait être utilisée pour détecter des particules mais ses performances seraient médiocres. Les paires électrons-trous créées dans l'épaisseur de la zone désertée, soumises à un champ faible, subiraient des phénomènes de recombinaison entre elles et avec les impuretés du réseau. D'autre part, l'épaisseur désertée étant faible, seule une fraction de l'énergie déposée par la particule pourrait être détectée.
Dans le cas où une polarisation inverse est appliquée (potentiel positif à la partie dopée n et négatif à la partie dopée p), les électrons (trous) libres sont attirés vers la partie extérieure du cristal polarisée positivement (négativement). Si la tension appliquée est suffisante, nous pouvons ainsi dépeupler de toute charge libre, l'épaisseur entière de la jonction p-n, voir Fig.3.4
Il devient donc possible de détecter le passage d'une particule dans une telle structure. Cependant, l'information recueillie concerne uniquement la perte d'énergie. La segmentation des électrodes (et donc de la jonction), qui correspond à l'idée de base des détecteurs en silicium à micropistes offre la possibilité d'obtenir, en plus de l'information sur la charge créée (et donc de l'énergie déposée) par le passage d'une particule, une information quant à son point de passage.
Dans les détecteurs à micropistes, la structure simple de la jonction p-n est reproduite sur une large surface. Dans le cas des détecteurs du SSD de STAR, le substrat de silicium (75 ![]() 42 mm
42 mm![]() et 300
et 300 ![]() m d'épaisseur) possède sur une face 768 implantations p
m d'épaisseur) possède sur une face 768 implantations p![]() qui sont autant de jonctions p-n, et sur l'autre face 768 implantations n
qui sont autant de jonctions p-n, et sur l'autre face 768 implantations n![]() que l'on appelle jonctions ohmiques. Cette double implantation, caractéristique des détecteurs double-face, permet d'assurer la collection des trous et des électrons. Chaque piste, jonction (p-n ou ohmique) est reliée à une voie de lecture électronique capable de lire la charge recueillie par cette structure.
Nous pouvons ainsi a la fois connaître le nombre de charges créées par le passage de la particule, donc sa perte d'énergie dans le substrat, ainsi que les pistes qui les ont recueillies, donc sa position.
que l'on appelle jonctions ohmiques. Cette double implantation, caractéristique des détecteurs double-face, permet d'assurer la collection des trous et des électrons. Chaque piste, jonction (p-n ou ohmique) est reliée à une voie de lecture électronique capable de lire la charge recueillie par cette structure.
Nous pouvons ainsi a la fois connaître le nombre de charges créées par le passage de la particule, donc sa perte d'énergie dans le substrat, ainsi que les pistes qui les ont recueillies, donc sa position.
Nous parlerons également de structures de test, ces objets sont en tous points identiques aux détecteurs décrits dans ce chapitre pour les caractéristiques électriques. Ils présentent deux différences majeures : un facteur d'échelle et un accès direct à l'implantation constituant les pistes. La réduction en taille diminue le nombre de pistes de 768 à 128 tout en gardant leur longueur constante.
![\begin{figure}
\centering\includegraphics[width=13cm,height=7cm,clip=true,draft=false]
{/home/suire/these/xfigure/Ssd/detection.eps} \end{figure}](img175.gif) |
Nous allons examiner maintenant les différents éléments qui composent les détecteurs en silicium double-face ainsi que leur impact son fonctionnement.
La méthode de polarisation des pistes se résume au choix de la résistance qui fera le lien (électrique) entre l'anneau de polarisation, sur lequel la tension de désertion est appliquée, et la piste implantée. La réalisation de cette résistance revêt une importance particulière car chaque technologie actuelle possède ses avantages et désavantages propres. Par exemple, les résistances en polysilicium demandent des niveaux de masques supplémentaires, et leur bonne tenue aux radiations va de paire avec un bruit plus élevé. Des études précises sont données dans les références suivantes, résistances polysilicium [Cac87,Edw91,Whe94], FoxFet [All91,Azz96], punch-through [Ell89,Hol89].
La méthode de polarisation, dite de punch-trough, qui est utilisée pour les détecteurs de STAR est illustrée schématiquement sur la figure 3.6.
Quand la tension appliquée atteint la valeur v, la zone désertée issue de l'anneau de polarisation entre en contact avec la zone désertée entourant la piste. Si la tension VCette méthode est simple à réaliser car elle ne demande pas de structure entre la piste et l'anneau. En revanche, la principale faiblesse concerne la tenue aux rayonnements ionisants.
![\includegraphics[width=9.5cm,height=10cm,clip=true,draft=false]
{/home/suire/these/xfigure/Ssd/electrical1.eps}](img180.gif) |
|
Représentée sur le schéma électrique simplifié ci-contre, cette capacité de couplage vaut 150 pF en moyenne (cf. section 4.1.1). La tension de polarisation, de l'ordre de 40 volts, est aussi appliquée sur la masse flottante de l'électronique de lecture. La différence de potentiel entre l'étage d'amplification et la piste du détecteur provient donc uniquement de la chute de tension dans la résistance de polarisation ( |
Trois cas, dépendant de l'état de la capacité de couplage, doivent être considérés:
Sans les détailler, nous pouvons citer les méthodes aujourd'hui employées afin d'améliorer la séparation ohmique entre les pistes de la face n.
Avec la technique dite des field-plate, la séparation est effectuée à l'aide d'un champ électrique qui repousse les électrons de la couche d'accumulation du voisinage de la piste. Pour créer ce champ, l'électrode de lecture (i.e la piste en aluminium) doit posséder une largeur supérieure à l'implantation n+.
![\begin{figure}
\includegraphics[height=6cm] {/home/suire/these/xfigure/Ssd/isolation.eps}\end{figure}](img181.gif) |
La technique des p-stop se résume à une (ou plusieurs) implantation p![]() supplémentaire entre chaque implantation n
supplémentaire entre chaque implantation n![]() . L'inconvénient majeur de cette solution est l'accroissement de la capacité interpiste et consécutivement du bruit. Il est établi que dans le cas d'une implantation p
. L'inconvénient majeur de cette solution est l'accroissement de la capacité interpiste et consécutivement du bruit. Il est établi que dans le cas d'une implantation p![]() de largeur (W
de largeur (W![]() ), la largeur apparente de l'implantation n
), la largeur apparente de l'implantation n![]() (W
(W![]() ) augmente fortement. La couche d'accumulation d'électrons se comporte comme une extension de l'implantation n
) augmente fortement. La couche d'accumulation d'électrons se comporte comme une extension de l'implantation n![]() , nous obtenons W
, nous obtenons W![]() = Pas interpiste - W
= Pas interpiste - W![]() .
.
La méthode d'isolation utilisée pour les détecteur en silicium du SSD est celle dite du p-spray. La face ohmique dans son ensemble reçoit une implantation de type p uniforme sur toute sa surface.
Le réseau capacitif présent dans les détecteurs en silicium gouverne la collection du signal ainsi que le couplage entre les pistes. C'est aussi une source importante de bruit électronique. Détaillons dans un premier temps les différentes capacités représentées sur la figure 3.7.
L'optimisation du rapport signal sur bruit passe par la définition d'une hiérarchie qui place en tête la collection du signal; soit C![]()
![]() C
C![]() car la charge lue par le préamplificateur est couplée par C
car la charge lue par le préamplificateur est couplée par C![]() .
.
Le rapport C![]() /C
/C![]() conditionne aussi la perte de signal. En effet, plus C
conditionne aussi la perte de signal. En effet, plus C![]() est grand par rapport à C
est grand par rapport à C![]() , plus le couplage s'effectuera entre une piste et ses voisines plutôt que vers la masse (perte du signal).
, plus le couplage s'effectuera entre une piste et ses voisines plutôt que vers la masse (perte du signal).
Le dernier point concerne la capacité vue par le préamplificateur C![]() : cette capacité est largement dominée par la capacité interpiste (C
: cette capacité est largement dominée par la capacité interpiste (C![]()
![]() C
C![]() + 2C
+ 2C![]() ). C
). C![]() doit donc être grand devant C
doit donc être grand devant C![]() et suffisamment petit pour ne pas augmenter exagérément le bruit.
et suffisamment petit pour ne pas augmenter exagérément le bruit.
De plus, le choix de la valeur de C![]() et donc de l'épaisseur d'oxyde est contraint par la tension de claquage. Nous voyons finalement que le réseau capacitif très complexe des détecteurs en silicium ne peut être simplement décomposé en capacités individuelles et indépendantes.
et donc de l'épaisseur d'oxyde est contraint par la tension de claquage. Nous voyons finalement que le réseau capacitif très complexe des détecteurs en silicium ne peut être simplement décomposé en capacités individuelles et indépendantes.
|
La figure 3.8 exhibe une dépendance avec la fréquence de mesure, dont une explication possible est apportée dans la référence [Bar94]. En examinant la figure 3.7, nous pouvons remarquer un filtre passe-bas formé par la résistance de polarisation et la capacité interpiste, qui a pour effet de couper les basses fréquences. Ce comportement semble tout à fait cohérent avec les mesures effectuées. La fréquence de coupure se situant à proximité de 6,5 kHz pour la face p et 2 kHz pour la face n, en supposant les valeur suivantes :
|
La mesure de la capacité interpiste a été effectuée pour toutes les pistes d'un détecteur, notamment dans le but de quantifier la présence de court-circuits entre les pistes implantées. Nous voyons sur la figure 3.9, qu'aucun défaut de ce genre n'a été constaté sur un détecteur de type STAR, justifiant, à posteriori, le choix de ne pas inclure ce test dans le protocole des tests de production.
Le circuit ALICE128C est le résultat d'un projet de développement pour la réalisation d'une électronique de lecture destinée à équiper les détecteurs en silicium des expériences ALICE et STAR. La définition de ce circuit est dictée par les besoins typiques aux expériences de collisions d'ions lourds ultra-relativistes. Les principales contraintes sont liées au nombre de particules issues de la collision et à l'énergie qu'elles déposent dans le détecteur et qui doit être traitée par la chaîne d'amplification de l'électronique. Les luminosités faibles atteintes dans les collisions d'ions lourds, au RHIC notamment, ne requièrent pas l'utilisation d'une électronique rapide. La référence [Feu00] donne une revue exhaustive des différents circuits de lecture disponibles pour les détecteurs en silicium à micropistes.
Le circuit ALICE128C a été choisi pour la lecture des détecteurs en silicium du SSD de STAR. Nous présenterons ici ses caractéristiques et fonctionnalités ainsi que des tests particuliers en vue de la caractérisation du module de détection.
L'analyse des données de tests sous faisceaux des modules de détection a permis de valider l'utilisation du circuit ALICE128C. En amont de cette validation, la caractérisation a été assurée par les concepteurs du circuit (LEPSI),[Heb97,Aya98].
Dans le cadre de l'expérience ALICE, la réalisation du nouveau circuit HAL025 répond d'une part aux inquiétudes sur le niveau de radiation attendu (estimé inférieur à 10 krad pour 10 ans de fonctionnement) et d'autre part à la définition d'un module de détection, différent de STAR, offrant d'autres solutions aux contraintes d'intégration, de connexion et de refroidissement. Ce circuit sera décrit à la fin de cette section.
Le circuit ALICE128, construit en technologie CMOS 1,2 ![]() m, a pour dimensions l = 6080
m, a pour dimensions l = 6080 ![]() m et L = 8640
m et L = 8640 ![]() m.
Les 128 voies d'entrées sont espacées d'un pas de 44
m.
Les 128 voies d'entrées sont espacées d'un pas de 44 ![]() m, chacune étant pourvue de 2 plots de connexion.
m, chacune étant pourvue de 2 plots de connexion.
De plus, un contrôleur JTAG permet la communication avec le circuit et l'accès à la plupart de ses fonctionnalités ainsi que la sélection des modes d'opérations (détaillés par la suite). Combiné à la présence d'un générateur de courant interne, ce système de contrôle offre des facilités remarquables pour le test et l'étalonnage.
La figure 3.11 montre un block diagram du circuit ALICE128C, c'est à dire l'organisation générale des parties actives ainsi que leurs interconnexions.
La lecture des pistes en mode séquentiel : c'est le mode utilisé pour l'acquisition des données du module de détection. Après la lecture des pistes, un signal externe (TOKENIN) déclenche la lecture du signal stocké dans C![]() . Le signal TOKENIN, véhiculé à la fréquence maximale de 10 MHz, ouvre successivement le trajet pour le signal de chaque canal vers le buffer de sortie commun.
. Le signal TOKENIN, véhiculé à la fréquence maximale de 10 MHz, ouvre successivement le trajet pour le signal de chaque canal vers le buffer de sortie commun.
La lecture d'une piste en mode transparent : ce mode de fonctionnement s'adapte particulièrement à la caractérisation d'une voie du circuit. Dans ce cas, un canal est sélectionné et lu en continu, c'est à dire que le signal n'est pas échantillonné dans la capacité C![]() . Nous voyons ainsi le signal à la sortie des blocs de préamplification et de mise en forme, se développer en fonction du temps.
. Nous voyons ainsi le signal à la sortie des blocs de préamplification et de mise en forme, se développer en fonction du temps.
L'envoi d'un signal test est possible dans les deux modes de fonctionnement séquentiel et transparent.
![\begin{figure}
\centering\includegraphics[width=16cm,height=6cm,clip=true,draft=false]
{/home/suire/Hardware/TestA128C/aout.eps} \end{figure}](img200.gif) |
La figure 3.12 montre la sortie analogique du circuit ALICE128C dans les deux modes de lecture avec une impulsion test envoyée sur une voie. En mode transparent, nous avons fait varier un des paramètres de polarisation du bloc de mise en forme. Le tracé en gras correspond à la valeur nominale de ce paramètre (91), ceux en pointillés à la variation autour de cette valeur (20,40,80,110,120,130). Cela montre la dépendance à la fois du temps de mise en forme (maximum d'amplitude) et du temps de descente (retour à la ligne de base ![]() 100 mV). Un ensemble de paramètres fourni par le LEPSI permet de retrouver les valeurs données dans le tableau 3.1.
100 mV). Un ensemble de paramètres fourni par le LEPSI permet de retrouver les valeurs données dans le tableau 3.1.
La lecture en mode séquentiel montre la lecture des 128 voies du circuit avec une impulsion test générée sur le canal 40. La ligne de base ou piédestal est constante à 100 mV. Nous pouvons aussi remarquer la présence d'une voie défectueuse (canal 90) pour laquelle la valeur du piédestal est nulle : ce défaut, inhérent au circuit, est crée lors de la réalisation du circuit par le fondeur.
Le contrôleur JTAG : compatible avec la norme IEEE1149.1-1990, il permet un contrôle complet du circuit à distance. Les principales fonctionnalités sont énumérées ci-dessous:
| polarité du courant(iDCin) < 0 pour la face n | |||
| polarité du courant(iDCin) > 0 pour la face p |
Afin de connaître le comportement de l'étage de préamplification dans un tel cas nous avons injecté un courant continu dans l'une des entrées du circuit en utilisant les facilités offertes par le TAB (voir chapitre suivant), qui fournit un accès très simple aux entrées du circuit.
Dans un même temps, ce canal était stimulé par une impulsion test du générateur interne et lu en mode transparent. L'amplitude du signal correspondant à l'impulsion test ainsi que le temps de mise en forme étaient ainsi vérifiés. La plus petite valeur mesurable du courant était i![]() = 0,1 nA.
= 0,1 nA.
Ainsi les défauts de rupture d'isolation vont induire des effets différents selon la face du détecteur à laquelle ils appartiennent. Dans les tests de production des détecteurs en silicium (cf. chapitre 4), nous déterminons les capacités de couplage défectueuses. Nous avons ainsi la possibilité de corréler ces informations après l'assemblage du détecteur en silicium à son électronique de lecture.
Nous obtenons donc le résultat représenté sur la figure 3.13. Considérant la gamme dynamique du générateur égale à 15 ![]() MIPs, nous obtenons un gain de 44,7
MIPs, nous obtenons un gain de 44,7![]() 0,1 mV/MIP en négligeant le terme constant de la droite d'ajustement. Cette valeur est inférieure de 6% aux spécifications du LEPSI précisant un gain d'environ 48 mV/MIP.
0,1 mV/MIP en négligeant le terme constant de la droite d'ajustement. Cette valeur est inférieure de 6% aux spécifications du LEPSI précisant un gain d'environ 48 mV/MIP.
La valeur du gain des circuits ALICE128C sera utilisé pour l'étalonnage de la chaîne d'acquisition des tests sous faisceaux (section 3.5). Nous choisirons la valeur théorique de 48 mV/MIP car le test décrit ici n'a pas été réalisé pour les circuits assurant la lecture des pistes des modules prototypes.
Les inquiétudes concernant le niveau de radiation dans l'expérience ALICE ont fortement motivé la conception d'un nouveau circuit résistant aux radiations. Le circuit présente une géométrie tout à fait différente du circuit ALICE128C. Dans un premier temps, le passage à la technologie 0,25 ![]() m qui est aujourd'hui un standard de l'industrie microélectronique, à permis une diminution de la surface totale. Ensuite, afin de faciliter la connexion par microcâbles entre les pistes d'un détecteur et les entrées analogiques, le pas entre les plots d'entrés est passé de 44 à 88
m qui est aujourd'hui un standard de l'industrie microélectronique, à permis une diminution de la surface totale. Ensuite, afin de faciliter la connexion par microcâbles entre les pistes d'un détecteur et les entrées analogiques, le pas entre les plots d'entrés est passé de 44 à 88 ![]() m. Les dimensions seront l = 10900
m. Les dimensions seront l = 10900 ![]() m et L = 3650
m et L = 3650 ![]() m.
m.
Les 128 entrées analogiques possèdent une diode de protection contre les décharges électrostatiques. Cette caractéristique n'existait pas pour le circuit ALICE128C et son absence a causé la destruction de canaux par décharge électrostatique pendant les opérations de connexions, que nous allons aborder dans le chapitre suivant. La sortie analogique du circuit devient un signal différentiel afin de minimiser le bruit parasite susceptible de se rajouter sur la ligne entre le circuit HAL025 et les cartes de conversion analogique-numerique (ADC). La gamme dynamique d'entrée a été conservée, mais le gain diminué d'un facteur 4.
Sur une demande spécifique d'ALICE, une remise à zéro rapide a été ajouté : celui-ci permet, quand un trigger de niveau supérieur rejette l'événement, de nettoyer tous les processus de lecture engagés.
Dans ce paragraphe, nous allons décrire les tests effectués afin de valider le procédé de connexion par TAB. Cette méthode d'interconnexion, présentée dans le chapitre 2, répond aux besoins exigés pour la connexion entre les pistes des détecteurs en silicium et leur électronique de lecture. Nous allons détailler maintenant le principe des tests effectués pour en extraire une valeur de l'efficacité de connexion [Sui01].
Dans les modules STAR, toutes les pistes du détecteur sont connectées aux voies d'électronique au moyen du ruban TAB. Ce procédé promet une efficacité de connexion supérieure à 99%, conditionnant ainsi l'efficacité de détection qui, pour les détecteurs en silicium à micropistes, diffère très peu du rapport entre le nombre de pistes inactives et le nombre de pistes total.
Le second point à vérifier concerne les connexions du circuit ALICE128C sur l'hybride, également effectuées par le TAB. Il y a 28 connexions à réaliser (qui véhiculent les signaux de contrôle) par circuit de lecture et la défaillance de l'une d'entre elle induit le dysfonctionnement du circuit et donc la perte de l'information provenant de 128 pistes du détecteur. En terme de détection de particules, il faut savoir que l'algorithme de reconstruction pour les modules de détection requiert un point sur chaque face pour la reconnaissance du passage d'une particule. La perte d'un circuit de lecture équivaut donc à une perte de 1/6 de la surface active du détecteur.
L'étude suivante vise à déterminer l'efficacité de connexion par la méthode TAB. Dans un premier temps pour valider ce nouveau procédé de connexion dans le cadre des modules de détection de STAR. Ensuite, l'extraction de la valeur de l'efficacité de connexion, convoluée au nombre de pistes et de voies d'électronique inactives, permettra d'estimer l'efficacité de détection pour un module.
Afin de comprendre les problèmes liés au TAB, on se reportera à la figure 3.14 illustrant les principales étapes du fonctionnement d'un canal d'acquisition. Quand une particule traverse le détecteur, des charges sont créées puis collectées sur les pistes sous l'action du champ électrique présent dans le substrat. Le signal ainsi formé est vu par le circuit de lecture à travers les pistes du ruban TAB (qui forment les connexions entre les pistes du détecteur et les entrées analogiques du circuit de lecture). Le signal est ensuite amplifié, mis en forme et stocké sous la forme d'une tension. Un multiplexeur analogique permet ensuite la lecture des 128 canaux, tensions qui sont numérisées dans un convertisseur analogique-digital et finalement écrites sur bande magnétique. Un signal de contrôle circulant séquentiellement à travers les 12 puces d'un détecteur, ordonne la lecture et permet ainsi de recueillir l'information provenant des 1536 pistes.
![\begin{figure}
\centering\includegraphics[width=12cm,height=14cm,clip=true,draft=false]
{/home/suire/xfigure/WholeChannel_bwfr.eps} \end{figure}](img204.gif) |
La méthode d'analyse explicitée ici vise à déterminer quels sont les problèmes induits par l'usage du TAB. Dans cette optique, nous allons dans un premier temps rechercher quelles variables extraites de l'analyse des données sont sensibles aux défauts de connexions. Nous entreprendrons ensuite une étude systématique des modules prototypes utilisant le TAB.
| (3.2) |
| (3.3) |
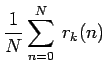 |
(3.4) | ||
![$\displaystyle \frac{1}{\sqrt{N - 1}} \sqrt{ \left\vert\sum_{n=0}^{N} \: \left[ ...
...n) \right]^2 \: - \: 1/N \left[ \sum_{n=0}^{N} \: r_k(n) \right]^2 \right\vert}$](img216.gif) |
(3.5) |
Nous allons utiliser ![]() calculé sur N = 900 événements, afin de déterminer les canaux présentant des défauts. La figure 3.15 illustre les résultats de ce calcul, pour les pistes de la face p d'un module prototype. Il apparaît que certains canaux montrent clairement une valeur supérieure ou inférieure à la moyenne.
Un test individuel de ces canaux va permettre de comprendre l'origine des problèmes. Grâce aux fonctionnalités du circuit ALICE128C, nous avons la possibilité de sélectionner une voie d'électronique et d'en faire la lecture en mode transparent (section 3.3). Deux moyens sont à notre disposition pour stimuler un canal :
calculé sur N = 900 événements, afin de déterminer les canaux présentant des défauts. La figure 3.15 illustre les résultats de ce calcul, pour les pistes de la face p d'un module prototype. Il apparaît que certains canaux montrent clairement une valeur supérieure ou inférieure à la moyenne.
Un test individuel de ces canaux va permettre de comprendre l'origine des problèmes. Grâce aux fonctionnalités du circuit ALICE128C, nous avons la possibilité de sélectionner une voie d'électronique et d'en faire la lecture en mode transparent (section 3.3). Deux moyens sont à notre disposition pour stimuler un canal :
![\begin{figure}
\centering\includegraphics[width=16cm,height=6cm,clip=true,draft=false]
{/home/suire/these/xfigure/TAB/zoom.eps} \end{figure}](img218.gif) |
Cas (a): ce canal (associé à la piste 487) fonctionne correctement; les signaux obtenus par stimulation avec la source ![]() et le générateur interne sont nominaux. Une valeur de
et le générateur interne sont nominaux. Une valeur de ![]() égale à
égale à ![]() coups ADC est obtenue.
coups ADC est obtenue.
Cas (b) : le canal (piste 480) fonctionne aussi correctement mais la valeur de ![]() est supérieure à la moyenne. C'est le comportement attendu et vérifié d'une piste bruyante.
est supérieure à la moyenne. C'est le comportement attendu et vérifié d'une piste bruyante.
Cas (c) : la réponse du canal (piste 481) à la stimulation par le générateur interne est nominale. En revanche, la source ![]() ne génère aucun signal en sortie du canal. L'explication la plus probable semble être une interruption entre la piste du détecteur et l'entrée du ALICE128C, et ce au niveau du TAB. Par conséquent, la valeur plus faible de
ne génère aucun signal en sortie du canal. L'explication la plus probable semble être une interruption entre la piste du détecteur et l'entrée du ALICE128C, et ce au niveau du TAB. Par conséquent, la valeur plus faible de ![]() confirme une diminution du bruit due au fait que la piste n'est pas connectée. De plus, un effet systématique apparaît dans ce cas, les pistes voisines
confirme une diminution du bruit due au fait que la piste n'est pas connectée. De plus, un effet systématique apparaît dans ce cas, les pistes voisines ![]() et
et ![]() présentent un bruit plus élevé.
présentent un bruit plus élevé.
Cas (d) : ce canal (piste 492) ne répond ni à la stimulation par le générateur interne ni à la stimulation par la source ![]() . La valeur de
. La valeur de ![]() se compare à celle obtenue dans le cas (c), cependant nous pouvons supposer ici que le problème s'apparente à la destruction de l'étage d'amplification pendant l'opération TAB. Aucun accroissement de bruit n'apparaît sur les pistes voisines.
se compare à celle obtenue dans le cas (c), cependant nous pouvons supposer ici que le problème s'apparente à la destruction de l'étage d'amplification pendant l'opération TAB. Aucun accroissement de bruit n'apparaît sur les pistes voisines.
Cas (e) : ce canal (piste 324) ne fonctionne pas. La sortie analogique est <<plate>> et ![]() très faible. L'ensemble de l'étage de préamplification et de mise en forme est certainement détruit. De tels canaux apparaissent sur le circuit pendant sa production et n'ont pas de relation avec le procédé de connexion, voir aussi la figure 3.12.
très faible. L'ensemble de l'étage de préamplification et de mise en forme est certainement détruit. De tels canaux apparaissent sur le circuit pendant sa production et n'ont pas de relation avec le procédé de connexion, voir aussi la figure 3.12.
Cas (f) : le circuit est inopérant, les pistes 129 à 256 ne sont pas lues. L'origine de ce problème se situe au niveau de la connexion par TAB entre le circuit et l'hybride. Une piste du ruban TAB transférant un signal de contrôle du circuit n'est pas connectée.
La figure 3.16 illustre les distributions de ![]() pour les différents cas détaillés ci-dessus. La valeur
pour les différents cas détaillés ci-dessus. La valeur ![]() est donnée par la RMS de la distribution.
est donnée par la RMS de la distribution.
Avant l'assemblage du module (connexion des différents éléments), chaque partie active subit des tests qui permettent de déterminer à quelles étapes les problèmes apparaissent. Nous présentons ici de façon détaillée les résultats pour le premier module (module 1).
| ||||||||||||||||||||||||||||||||||||||
Après connexion et assemblage, le module 1 a subi la procédure de test décrite ci-dessus. Nous avons ainsi déterminé les canaux présentant des défauts : le tableau 3.3 résume les résultats obtenus.
Les défauts de connexion ont ainsi été déterminés pour les quatre modules. Ils sont présentés sur la figure 3.18 en fonction de l'indice de la piste du ruban TAB (numéro de la piste modulo 128). Pour les modules 2 et 3, il n'y a pas de résultats pour l'analyse de la face n.
![\begin{figure}
\centering\includegraphics[width=17cm,height=14cm,clip=true,draft=false]
{/home/suire/these/xfigure/TAB/StripNCTAB_all.eps} \end{figure}](img225.gif) |
Nous voyons clairement, grâce à ce type de représentation, apparaître une corrélation entre le type de défaut et leur localisation sur le ruban TAB. Les pistes non-connectées sont localisées sur quatre zones distinctes, soit en terme d'indice de pistes du ruban à (1,2,3... ), (128,127,126,... ) et autour de 32 et 97. Ces zones correspondent à des connexions sur les bords du ruban ou du circuit ALICE128C.
En revanche, les défauts liés à des préamplificateurs inopérant semblent se répartir de manière aléatoire. L'explication la plus raisonnable concernant l'occurence de ces défauts réside dans la possibilité de décharges électrostatiques (ESD) aux entrées analogiques du circuit ALICE128C. Le tableau 3.4 résume cette analyse en terme d'efficacité de connexion.
Nous pouvons caractériser globalement la qualité de la connexion par TAB ainsi:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Nous obtenons une efficacité moyenne de connexion par la méthode TAB de 98% en ne tenant pas compte de la perte introduite lorsqu'un circuit est inopérant. Cette estimation semble satisfaisante dans le cadre des premiers prototypes qui ont servi à la mise en place des différentes opérations de connexions.
La présence d'un circuit inopérant qui introduit une perte d'efficacité de 16,6%, n'existe déjà plus pour les modules prototypes 5 et 6. En effet, les connexions allant du circuit vers l'hybride sont les plus simples à réaliser (la taille et l'espacement des plots de connexion sont élevés, de l'ordre de ![]() m).
m).
De plus, les problèmes liés aux pistes non-connectées et à la destruction des préamplificateurs par des décharges électrostatiques sont maintenant connus et pris en compte par l'entreprise qui réalise le TAB. Nous pouvons ainsi viser une efficacité de connexion pour les futurs modules supérieure à 98%. Le procédé TAB lorsqu'il a été choisi pour les modules STAR promettait un taux intrinsèques de mauvaises connexions de 0.1%.
Dans le cadre de l'expérience ALICE, et au bénéfice de ces tests, un développement commun du ruban de connexion et du nouveau circuit HAL025 doit résoudre ces problèmes par l'utilisation des diodes de protections pour les entrées du circuit de lecture et une nouvelle topologie des pistes du ruban (disparition des pistes courbées) adaptée à une distance entre les entrées du circuit plus élevée (passage de 44 ![]() m à 80
m à 80 ![]() m).
m).
Le protocole de test utilisé lors de cette analyse n'est pas transposable au test de production des modules. Un banc de test dédié utilisant une source laser et un système d'acquisition de données plus simple, est à présent opérationnel et permet déjà d'obtenir des résultats.
Le dernier point à mentionner concerne une étude menée sur les corrélations de bruit des modules utilisant le TAB. Les résultats montrent qu'il n'existe aucune différence significative entre un détecteur câblé par fil ou par ruban TAB [Pin00].
Le télescope utilisé lors des tests sous faisceau est représenté schématiquement sur la figure 3.19. Il se constitue de huit plans de détecteurs en silicium simple-face à micropistes. Chacun comporte 256 pistes espacées de 50 ![]() m, implantées dans un substrat de type n. La surface active est de 12.8
m, implantées dans un substrat de type n. La surface active est de 12.8![]() 12.8 mm
12.8 mm![]() et l'épaisseur de 300
et l'épaisseur de 300 ![]() m. Dans le module 1, les détecteurs possèdent une piste intermédiaire flottante entre les pistes de lecture [Kot85], et deux dans le module 2. L'électronique de lecture utilisée est le circuit VA2. Le module de détection à tester est inséré entre les modules 1 et 2.
m. Dans le module 1, les détecteurs possèdent une piste intermédiaire flottante entre les pistes de lecture [Kot85], et deux dans le module 2. L'électronique de lecture utilisée est le circuit VA2. Le module de détection à tester est inséré entre les modules 1 et 2.
![\begin{figure}
\centering\includegraphics[width=15cm,clip=true,draft=false]
{/home/suire/these/xfigure/BeamTest/setup_test_alice_f.eps} \end{figure}](img227.gif) |
Les pistes d'un plan de référence sont orientées verticalement (plans X) ou horizontalement (plans Y) comme indiqué sur le schéma. Lors du passage d'une particule à travers le télescope, nous pouvons ainsi recueillir 4 couples de coordonnées (X,Y), et par interpolation linéaire reconstruire la trace de la particule. Deux scintillateurs plastiques de 7![]() 7 mm
7 mm![]() (cette surface définit également la taille apparente du faisceau), couplés à des photo-multiplicateurs sont utilisés pour signer le passage d'une particule. Les signaux reçus en coïncidence déclenchent le système d'acquisition (trigger).
(cette surface définit également la taille apparente du faisceau), couplés à des photo-multiplicateurs sont utilisés pour signer le passage d'une particule. Les signaux reçus en coïncidence déclenchent le système d'acquisition (trigger).
| (3.6) |
| (3.8) |
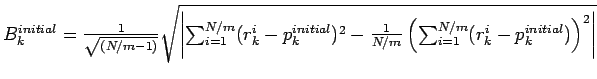 |
(3.9) |
Le déplacement de mode commun, cms3.7 se calcule par événement et par circuit de lecture, le déplacement étant commun pour tous les canaux d'un même circuit lors de l'événement ![]() .
.
| (3.10) |
| (3.11) |
| (3.13) |
![$ B_k(n) = \sqrt{ \frac{1}{W_b} \left[ (W_b - 1) {B_k(n-5)}^2 + {q_k^{rnd}(n')}^2 \right]} \quad n \geq n'> n-5$](img241.gif) |
(3.14) |
| Piste graine ou centrale : |
|||
| Pistes voisines : |
| (3.15) |
Méthode digitale
La méthode digitale fournie, pour valeur de ![]() , la position de la piste centrale
, la position de la piste centrale ![]() de l'amas.
de l'amas.
| (3.16) |
Méthode du centre de gravité
Cette méthode utilise toute les pistes incluses dans l'amas (centrale et voisines).
| (3.17) |
| (3.18) |
Méthode ![]() non-linéaire
non-linéaire
Si l'on observe la distribution ![]() pour les détecteurs de références ou testés, nous pouvons remarquer que celle-ci n'est pas constante (figure 3.21). Toutes les valeurs de
pour les détecteurs de références ou testés, nous pouvons remarquer que celle-ci n'est pas constante (figure 3.21). Toutes les valeurs de ![]() ne sont pas équiprobables,
traduisant une collection de charges non-linéaire dépendant de la position de l'impact de la particule entre les pistes.
La méthode
ne sont pas équiprobables,
traduisant une collection de charges non-linéaire dépendant de la position de l'impact de la particule entre les pistes.
La méthode ![]() non-linéaire tient compte des ces disparitées.
non-linéaire tient compte des ces disparitées.
| (3.19) |
| (3.20) |
![\begin{figure}
\centering\includegraphics[width=14cm,height=6cm,clip=true,draft=false]
{/home/suire/these/plot/eta.eps} \end{figure}](img259.gif) |
Les différentes méthodes de calcul détaillées ci-dessus sont tout d'abord appliquées à la reconstruction du signal (amas de charges) dans les détecteurs de références. La deuxième étape consiste en la reconstruction de la trace de la particule, à partir des informations (positions des amas de charges) recueillies sur les plans de référence, qui s'effectue simultanément avec la procédure d'alignement du télescope.
![\begin{figure}
\centering\includegraphics[height=7cm]{/home/suire/these/plot/rawdataPlan3.eps} \end{figure}](img260.gif) |
A titre d'exemple pour le plan de référence 3, les distributions des variables d'analyse que sont le piédestal, le déplacement de mode commun ainsi que le bruit sont représentées sur la figure 3.23.
En (a), les données brutes (prenant les valeurs entières entre 50 et 56 coups ADC) pour une piste du plan de référence 3 située hors du faisceau, et qui n'a donc pas reçu de signal dû au passage d'une particule. Sur la même figure, la valeur calculée du piédestal au cours du temps (equivalent au nombre d'événements). En (b), la différence entre les données brutes et le piédestal de cette même piste. Comme cette piste n'est pas située dans le faisceau, la variance de cette distribution correspond au bruit de la piste (à la correction du déplacement de mode commun près). Nous voyons l'effet du a la soustraction de la valeur non-entière du piédestal à la valeur entière après numérisation du signal brut, et la dispersion consécutive autour des 3 pics localisés en 0 etNous retrouvons par un calcul simple que le déplacement de mode commun et le bruit d'une piste sont des quantités indépendantes, donc qui s'ajoutent quadratiquement:
Afin de reconstruire le signal dû au passage d'une particule, nous devons choisir des valeurs pour les différents seuils qui séparent, au niveau d'une piste, un événement bruit d'un événement signal.
| Piste centrale : |
|||
| Pistes voisines : |
|||
| Taille maximale : |
Ces valeurs optimisent les résultats même si leur dépendance par rapport aux coupures utilisées est faible.
Sur la figure 3.24, nous voyons le signal reconstruit après analyse des données pour le plan 3. Il s'agit du signal reconstruit pour des pions au minimum d'ionisation traversant un détecteur en silicium de 300 ![]() m d'épaisseur. Le maximum de la distribution de Landau associée est de 52 coups ADC.
m d'épaisseur. Le maximum de la distribution de Landau associée est de 52 coups ADC.
Cette analyse a été effectuée pour les plans de référence secondaires (ce terme sera expliqué dans le paragraphe suivant) : le tableau 3.5 résume les différentes valeurs obtenues pour le maximum de probabilité de la perte d'énergie, le bruit, et le rapport signal sur bruit moyen.
|
Les valeurs de bruit obtenues sont faibles : les détecteurs de référence sont, comme nous l'avons vu, constitués de détecteurs en silicium simple face équipés d'une électronique de lecture à bas bruit (circuit VA2). Ces raisons expliquent en grande partie les excellentes valeurs du rapport signal sur bruit obtenues pour les plans de référence et en conséquence une excellente efficacité de reconstruction des traces dans le télescope.
Dans le cas le plus général, nous pouvons dénombrer 6 paramètres de désalignement par rapport à une position parfaite du détecteur dans le télescope, 3 translations et 3 rotations. La figure 3.19 donne une représentation des différents repères utilisés : le repère global (
![]() ) est lié au système du télescope, le repère local (
) est lié au système du télescope, le repère local (
![]() ) est, quant à lui, propre à un plan de référence. Les vecteurs
) est, quant à lui, propre à un plan de référence. Les vecteurs
![]() et
et
![]() sont colinéaires et orientés selon l'axe du faisceau.
Nous allons considérer que les plans de référence 1, 2, 5 et 6 sont à la fois parallèles entre-eux et tous orthogonaux à l'axe du faisceau : ils fournissent 2 couples de coordonnées (X,Y) absolus. Ils seront qualifiés par le terme références primaires par opposition aux plans 3, 4, 7 et 8, dits références secondaires que nous allons aligner en fonction des informations données par les références primaires.
Le passage du système de coordonnées locales au système global s'effectue grâce à la transformation suivante :
sont colinéaires et orientés selon l'axe du faisceau.
Nous allons considérer que les plans de référence 1, 2, 5 et 6 sont à la fois parallèles entre-eux et tous orthogonaux à l'axe du faisceau : ils fournissent 2 couples de coordonnées (X,Y) absolus. Ils seront qualifiés par le terme références primaires par opposition aux plans 3, 4, 7 et 8, dits références secondaires que nous allons aligner en fonction des informations données par les références primaires.
Le passage du système de coordonnées locales au système global s'effectue grâce à la transformation suivante :
Reconstruction des traces
Un ajustement linéaire des coordonnées
![]() , positions des amas de chaque plan permet de déterminer l'origine et la pente de la trajectoire. Dans la phase d'alignement, seules les références primaires sont utilisées (plans 1, 2, 5 et 6). Dans la phase de reconstruction des traces proprement dite, nous utilisons tous les plans de références (plans 1, 2, 3, 4, 5, 6, 7 et 8).
Un estimateur moindre carré est construit à partir des vecteurs des positions mesurées par chaque plan de référence:
, positions des amas de chaque plan permet de déterminer l'origine et la pente de la trajectoire. Dans la phase d'alignement, seules les références primaires sont utilisées (plans 1, 2, 5 et 6). Dans la phase de reconstruction des traces proprement dite, nous utilisons tous les plans de références (plans 1, 2, 3, 4, 5, 6, 7 et 8).
Un estimateur moindre carré est construit à partir des vecteurs des positions mesurées par chaque plan de référence:
Alignement
La procédure d'alignement vise à déterminer les variables ![]() et
et
![]() , pour chaque plan de référence secondaire. Dans un premier temps, on forme une trace au moyen des points donnés par les références primaires, cela nous permet d'obtenir une position reconstruite
, pour chaque plan de référence secondaire. Dans un premier temps, on forme une trace au moyen des points donnés par les références primaires, cela nous permet d'obtenir une position reconstruite
![]() pour chaque plan à aligner. Nous pouvons ensuite calculer la différence entre la position de l'amas et la position reconstruite,
pour chaque plan à aligner. Nous pouvons ensuite calculer la différence entre la position de l'amas et la position reconstruite, ![]() .
.
![\begin{figure}
\centering\includegraphics[width=10cm,height=10cm,clip=true,draft=false]
{/home/suire/these/xfigure/BeamTest/align.eps} \end{figure}](img281.gif) |
Cela se traduit par une distribution des résidus ![]() centrée à zéro (compensation du décalage dans la direction perpendiculaire aux pistes) et l'invariance de la distribution
centrée à zéro (compensation du décalage dans la direction perpendiculaire aux pistes) et l'invariance de la distribution ![]() en fonction de la position de la trace parallèlement aux pistes (pente
en fonction de la position de la trace parallèlement aux pistes (pente
![]() égale à 1).
égale à 1).
![\begin{figure}
\centering\includegraphics[width=15cm,height=20cm,clip=true,draft=false]
{/home/suire/these/plot/plotAlgnResult300bis.eps} \end{figure}](img293.gif) |
La quantité ![]() définie par l'équation 3.24 correspond à l'erreur faite sur la reconstruction de la trace au niveau d'un plan de détection. Nous pouvons ainsi obtenir la déviation standard de cette distribution.
définie par l'équation 3.24 correspond à l'erreur faite sur la reconstruction de la trace au niveau d'un plan de détection. Nous pouvons ainsi obtenir la déviation standard de cette distribution.
Dans le cas des détecteurs de référence (primaires et secondaires), la résolution intrinsèque est de 1.35 ![]() m dans le meilleur des cas en utilisant l'algorithme
m dans le meilleur des cas en utilisant l'algorithme ![]() non-linéaire. Dans cette analyse, nous avons obtenu des valeurs de résolution intrinsèque
non-linéaire. Dans cette analyse, nous avons obtenu des valeurs de résolution intrinsèque
![]() proches de 2,5
proches de 2,5 ![]() m.
m.
Les caractéristiques des modules testés sont décrites dans le chapitre 2. Elles ont, comme nous l'avons vu, évolué de manière significative au cours des différents tests sous faisceau. Les premiers modules testés se constituaient des premiers prototypes de détecteur en silicium double-face et du circuit ALICE128 avec une connexion classique par fil [Sui99]. Nous avons ensuite construit les modules de détection aux spécifications du SSD de STAR en utilisant la connexion par TAB. Des résultats de tests sous faisceaux pour ces deux types de modules seront présentés.
Dans les paragraphes suivants, nous décrirons les méthodes de calculs appliquées au cas spécifique des détecteurs à micropistes que nous utilisons. Dans un premier temps, l'analyse consiste en une étude de chaque face considérée indépendante : reconstruction des amas de charge et résolution en position à une dimension. Les résultats obtenus sont finalement associés afin de déterminer les résolution en position et en énergie du module.
 |
Le principal objectif dans la recherche d'une méthode performante de calcul du bruit se résume à exclure le signal physique dû à une particule sans introduire de biais (qui généralement tend à sous-estimer le bruit). Une solution évidente consisterait en l'utilisation de données prise en l'absence de faisceau. Le calcul du piédestal et de sa variance (le bruit) ne seront donc en aucun cas biaisé par la présence de signal physique dû à une particule. Le problème est que nous ne disposons pas toujours de telles données.
La première méthode (utilisée pour les plans de référence) est basée sur une mémoire tampon dans laquelle sont rangées les valeurs des données brutes. Une valeur en est extraite à condition qu'elle ne soit pas la plus grande valeur du tableau, puis est utilisée pour le calcul du piédestal.
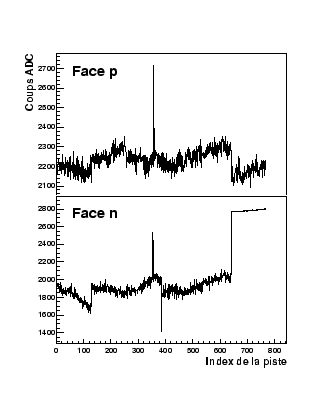
La méthode choisie utilise un ajustement par une gaussienne de la valeur calculée du signal de la piste. Ainsi le signal physique provenant du passage d'une particule n'est pas pris en compte car sa valeur, plus élevée, est située hors de la gaussienne. La figure 3.29 montre le bruit calculé pour les 768 pistes des faces p et n d'un module par cette méthode. De ces distributions, nous avons pu extraire le bruit moyen des pistes sur une face ainsi que le nombre de pistes bruyantes, qui par définition possèdent un bruit deux fois supérieur au bruit moyen de la face.
Ces deux méthodes fournissent des résultats comparables pour les pistes hors du faisceau. En revanche, pour les pistes situées dans le faisceau (entre les pistes d'index 340 à 440), le biais dû au signal d'une particule est complètement éliminé par la méthode utilisant l'ajustement par une gaussienne.
Nous pouvons également mentionner une autre méthode utilisant la reconstruction des traces. Après la phase d'alignement, nous connaissons le point de passage de la particule dans le détecteur. Cette information est ensuite utilisée afin d'exclure du calcul du bruit les pistes dans la proximité du point de passage de la particule. Cette méthode est performante mais présente un inconvénient substantiel : elle nécessite de posséder par avance l'information sur la reconstruction de la trace. Elle n'est donc utilisable que dans le cadre de tests sous faisceau utilisant le télescope.
Une dernière méthode envisageable, sans doute la meilleure, consisterait en l'utilisation de données prises sans particules entre les arrivées du faisceau sur le détecteur. Le calcul du piédestal et de sa variance (le bruit) pourrait être effectué sans la crainte d'inclure le signal dû à une particule. Cela nécessite néanmoins une modification du système d'acquisition, ainsi que le marquage des événements sans particules afin qu'ils puissent être identifiés lors de l'analyse comme étant ceux dédiés au calcul du piédestal et du bruit. Cette méthode présenterait également l'avantage de calculer le bruit tout au long de la prise de données, assurant le suivi des fluctuations. Cette méthode est très largement comparable à celle qui sera utilisée lors de la prise de données du SSD installé dans STAR.
Les coupures utilisées pour la reconstruction du signal pour les modules de détection sont les suivantes :
| Piste centrale : |
|||
| Pistes voisines : |
|||
| Taille maximale : |
Sur la figure 3.24, la charge totale des amas est reconstruite pour les faces p et n du détecteur.
Les valeurs les plus probables pour la perte d'énergie d'une particule au minimum d'ionisation sont de 253 et 292 coups ADC respectivement pour les faces p et n. Nous pouvons normaliser ces valeurs par rapport à la charge attendue de 25000 électrons pour une particule au minimum d'ionisation (MIP) traversant 300 ![]() m de silicium.
m de silicium.
Les valeurs différentes obtenues s'expliquent par un gain inégal sur les chaînes d'électroniques assurant la lecture des faces p et n. Nous pourrions également incriminer une perte de signal sur la face p ou inversement le surestimer sur la face n. Un étalonnage de la chaîne d'acquisition réalisé suite aux tests sous faisceau a confirmé l'existence d'une différence de gain entre les chaînes d'électroniques. Les distributions expérimentales sont ajustées par la convolution d'une distribution de Landau avec une gaussienne [Han83].
![\begin{figure}
\centering\includegraphics[width=12cm,height=9cm,clip=true,draft=false]
{/home/suire/these/plot/300PNcharge.eps} \end{figure}](img302.gif) |
Nous pouvons maintenant extraire une valeur du signal sur bruit (S/N). Formellement, pour obtenir le S/N, il faudrait diviser la charge totale reconstruite d'un amas par la somme quadratique du bruit des pistes constituant cet amas. Si l'on considère que le bruit est égal à une constante pour les ![]() pistes de l'amas, ce calcul rend la valeur du S/N dépendante du nombre de pistes d'un facteur inversement proportionnel à
pistes de l'amas, ce calcul rend la valeur du S/N dépendante du nombre de pistes d'un facteur inversement proportionnel à
![]() . Nous définirons le rapport S/N comme le signal total reconstruit divisé par le bruit de la piste centrale et uniquement celle-ci. En contrepartie, cette définition surestime la valeur de S/N.
. Nous définirons le rapport S/N comme le signal total reconstruit divisé par le bruit de la piste centrale et uniquement celle-ci. En contrepartie, cette définition surestime la valeur de S/N.
Les distributions du rapport S/N sont représentées sur la figure 3.31. Le tableau 3.6 résume ces différentes valeurs obtenues pour cette analyse (mp signifie qu'on se situe maximum de probabilité).
|
Un nombre égal de charges positives et négatives sont crées dans le silicium par l'ionisation due à une particule. Les charges totales des amas (Q![]() et Q
et Q![]() ) reconstruits peuvent cependant être différentes. Nous définissons ici la résolution en énergie comme l'écart entre une corrélation de charge parfaite (Q
) reconstruits peuvent cependant être différentes. Nous définissons ici la résolution en énergie comme l'écart entre une corrélation de charge parfaite (Q![]() = Q
= Q![]() ) et celle effectivement mesurée.
) et celle effectivement mesurée.
Afin d'obtenir une valeur exacte, i.e. non biaisée par de fausses associations entre des amas des faces p et n , nous vérifions dans un premier temps l'écart (en terme d'indice de pistes) entre la piste centrale relativement à l'amas reconstruit sur la face p et celle relative à l'amas reconstruit sur la face n. Nous avons vu précédemment que cette différence ne peut pas être supérieure à 15 et donc définit notre critère de sélection.
Nous avons déterminé la droite de corrélation parfaite par un ajustement linéaire, afin de calculer la déviation par rapport à celle-ci. Nous observons cependant une pente qui n'est pas unitaire, traduisant la différence de gain entre les chaînes d'électroniques des deux faces. La déviation obtenue est de 12 coups ADC : en se plaçant à une charge collectée proche du MIP pour les deux faces, par exemple 270 coups ADC, nous voyons alors que cette déviation ne représente que 4% de la charge totale reconstruite. Le bruit du détecteur est le facteur prépondérant qui dégrade la résolution en énergie car il influence la reconstruction du signal différemment sur les faces p et n.
![\begin{figure}
\centering\includegraphics[width=10cm,height=6cm,clip=true,draft=false]
{/home/suire/these/xfigure/BeamTest/detgeo_bw.eps} \end{figure}](img308.gif) |
La procédure d'alignement choisie pour les détecteurs double-face s'applique à considérer les deux faces indépendantes. Nous pouvons voir sur la figure 3.33 les repères associés à chaque face qui sont utilisés lors de l'alignement : chaque plan (U,V) est orienté de manière à ce que la direction U soit orthogonale aux pistes de la face considérée. Nous parlerons donc de résolution (intrinsèque) dans la direction U pour les faces p et n d'un détecteur double-face, et de résolution en Z et r![]() pour le détecteur dans son ensemble après l'association des positions données par chacune des faces.
pour le détecteur dans son ensemble après l'association des positions données par chacune des faces.
Les différents repères étant définis, nous pouvons maintenant exprimer la transformation permettant le passage des repères associés aux pistes (U,V) et celui associé au module (r![]() ,Z) dont les vecteurs unitaires sont notés (
,Z) dont les vecteurs unitaires sont notés (
![]() ,
,
![]() ). Nous supposons également l'origine de ces repères commune et fixée en un point O (centre du détecteur).
). Nous supposons également l'origine de ces repères commune et fixée en un point O (centre du détecteur).
Un indice fort d'un bon alignement est alors donné par l'angle de rotation relatif entre les deux faces qui doit égaliser l'angle stéréoscopique. Lors de cet alignement, la valeur de 2,0 degré a été obtenue soit exactement l'angle stéréoscopique de 35 mrad.
| (3.32) |
Nous pouvons remarquer la structure particulière de ces distributions, marquée plus nettement sur la face p, avec la présence de pics pour des valeurs de résidu autour de ![]() 30
30 ![]() m. Ce phénomène devient facilement explicable en utilisant une représentation différente. Nous avons reporté sur la figure 3.35 la distribution du résidu de la face en fonction de la distance à la piste la plus proche, cette piste étant désignée en utilisant uniquement l'information liée à la trace reconstruite par le télescope.
m. Ce phénomène devient facilement explicable en utilisant une représentation différente. Nous avons reporté sur la figure 3.35 la distribution du résidu de la face en fonction de la distance à la piste la plus proche, cette piste étant désignée en utilisant uniquement l'information liée à la trace reconstruite par le télescope.
![\begin{figure}
\centering\includegraphics[width=8cm,height=8cm,clip=true,draft=false]
{/home/suire/these/plot/300PresForme.eps} \end{figure}](img324.gif) |
Nous voyons apparaitre clairement deux structures : la première est la ligne correspondant à la représentation du cas où l'amas est constitué par une seule piste, c'est le cas de la résolution digitale. La valeur du résidu est donc égale à la distance entre la position de l'amas reconstruit, i.e. la position de la piste, et la position réelle de l'amas : nous obtenons une droite d'équation y = x dans notre représentation.
La deuxième structure est constituée par tous les autres points, pour lesquels plusieurs pistes composent l'amas reconstruit. Nous voyons que la valeur du résidu commence à diminuer pour des distances supérieures à 25 ![]() m, distances qui définissent la zone de partage effectif de charges pour nos détecteurs en silicium. Nous voyons cependant qu'au delà de cette zone, l'erreur sur la position reconstruite reste importante (résidu
m, distances qui définissent la zone de partage effectif de charges pour nos détecteurs en silicium. Nous voyons cependant qu'au delà de cette zone, l'erreur sur la position reconstruite reste importante (résidu
![]() m). Ceci constitue l'explication aux pics présents sur la figure 3.35.
m). Ceci constitue l'explication aux pics présents sur la figure 3.35.
La méthode du centre de gravité impose certaines limites à la reconstruction spatiale du point d'impact que nous allons préciser. Son principal défaut repose sur l'hypothèse implicite que si un point d'impact est localisé entre deux pistes alors le rapport des charges collectées sur ces pistes est proportionnel à la distance entre le point et l'une des pistes, donc un comportement linéaire du partage de charge.
Le partage de charge dans ces détecteurs a été caractérisé dans la référence [Ret00], cette étude montre que l'utilisation d'un algorithme basé sur la distribution ![]() permet d'améliorer significativement la résolution en incidence normale. Cependant si l'angle d'incidence de la particule dans le détecteur n'est pas nul, alors l'algorithme du centre de gravité est également performant.
permet d'améliorer significativement la résolution en incidence normale. Cependant si l'angle d'incidence de la particule dans le détecteur n'est pas nul, alors l'algorithme du centre de gravité est également performant.
Appliquant la transformation régie par l'équation 3.31, nous accédons aux distributions des résidus dans le plan (r![]() ,Z) du référentiel du détecteur. A partir de cette même équation, nous pouvons déterminer les résolutions attendues dans le plan (r
,Z) du référentiel du détecteur. A partir de cette même équation, nous pouvons déterminer les résolutions attendues dans le plan (r![]() ,Z) :
,Z) :
De plus, le dispositif de contrôle, voir la figure 3.20, a été rendu le plus proche possible de celui qui sera utilisé dans STAR. Ainsi le châssis CAEN fournissant les tensions d'alimentations était placé à une distance de l'ordre de 30 mètres. La différence majeure se situe au niveau de l'acquisition. Dans STAR les données provenant de la face flottante (la face portée au potentiel de polarisation du détecteur) seront numérisées par des convertisseurs eux aussi flottant, ensuite seulement une translation de niveau, via un couplage opto-électronique, sera réalisée. Cette caractéristique devrait permettre de minimiser le bruit dû au passage par un opto-coupleur car les données numérisées sont bien évidemment moins sensibles au bruit que les données analogiques. De plus, le passage par les composants électroniques qui composent un opto-coupleur est une source de bruit. Lors des tests sous faisceau, le passage par l'opto-coupleur s'effectue avant la numérisation du signal, la charge équivalente de bruit ajoutée a été estimé à environ 150 électrons.
Les maximums de probabilité des distributions de Landau de la charge totale des amas pour les faces p et n sont respectivement de 148 et 139 coups ADC.
Etalonnage de la chaîne d'acquisition
La chaîne d'électronique en sortie véhiculant le signal analogique de sortie du circuit ALICE128C a été étalonnée. Le principe est très simple : un signal d'amplitude et de fréquence choisies (signal triangulaire d'amplitude 600 mV crête à crête et de fréquence 5kHz) est injecté dans la chaîne en lieu et place de la sortie analogique du circuit. Après l'analyse de ces données, la relation entre la tension injectée et les valeurs ADC peut être établie. Les résultats sont présentés dans le tableau 3.7.
|
Deux informations sont à extraire de ce tableau : le signal collecté correspond effectivement au signal attendu si l'on considère le gain du circuit ALICE128C, 48 mV pour une particule au MIP. Nous obtenons également la relation d'équivalence entre l'unité ADC et le nombre d'électrons, nécessaire pour exprimer des valeurs absolues de charge équivalente de bruit.
|
Nous avons reporté dans le tableau 3.8 les résultats en terme de signal et de bruit pour les faces p et n. L'augmentation du bruit, en comparaison du module prototype, est liée au passage simultané à la connexion par TAB et donc à l'utilisation des circuits hybrides finaux. Les contributions respectives n'ont pu être isolées séparément. Le nombre de pistes bruyantes reste faible. Il faut néanmoins noter la présence sur ce module d'une zone bruyante qui provoque, sur environ 15 pistes adjacentes de chaque face (qui ne sont pas comptabilisées dans le tableau 3.8), un bruit plus important. Cette zone bruyante provient d'un défaut intrinsèque au détecteur en silicium.
La figure 3.38 montre les distributions du signal sur bruit pour les faces p et n du module de détection.
Les valeurs de résolution en position pour ce prototype STAR sont résumées dans le tableau 3.9 suivant :
|
La définition de l'efficacité employée dans cette analyse est la suivante : la trace est dans un premier temps reconstruite au moyen du télescope, puis extrapolée sur les faces p et n du module de détection (préalablement aligné). Deux positions, notées ![]() et
et ![]() , sont obtenues ainsi que les index des pistes les plus proches du point d'impact
, sont obtenues ainsi que les index des pistes les plus proches du point d'impact ![]() et
et ![]() .
Nous définissons également 3 seuils :
.
Nous définissons également 3 seuils :
La figure 3.39 montre l'évolution de l'efficacité en fonction du seuil en signal sur bruit, avec T![]() 30 (
30 (![]() 4
4![]() ) et T
) et T![]() =
= ![]() 200
200 ![]() m autour du point d'impact reconstruit. Il faut préciser qu'une zone fiduciaire a été définie afin de s'affranchir des pistes inactives, permettant d'atteindre une efficacité de 100%. Ces pistes inactives ont été déterminées au moyen du test des connexions par TAB décrit dans la section 3.4.
m autour du point d'impact reconstruit. Il faut préciser qu'une zone fiduciaire a été définie afin de s'affranchir des pistes inactives, permettant d'atteindre une efficacité de 100%. Ces pistes inactives ont été déterminées au moyen du test des connexions par TAB décrit dans la section 3.4.
Ces tests sous faisceaux ont permis une étude détaillée des performances des détecteurs en silicium ainsi que leur évolution au cours de la définition et construction du module STAR tel qu'il existe dans sa version finale.
La résolution intrinsèque des détecteurs est de ![]()
![]() 22
22 ![]() m, pour des particules au minimum d'ionisation en incidence normale. Cette valeur peut être améliorée en fonction de l'algorithme de reconstruction du signal choisi.
Les résolutions dans les directions r
m, pour des particules au minimum d'ionisation en incidence normale. Cette valeur peut être améliorée en fonction de l'algorithme de reconstruction du signal choisi.
Les résolutions dans les directions r![]() (plan transverse) et Z (axe du faisceau) après la reconstruction du signal sur chaque face sont
(plan transverse) et Z (axe du faisceau) après la reconstruction du signal sur chaque face sont
![]() 16
16 ![]() m et
m et
![]() 890
890 ![]() m.
La charge équivalente de bruit pour une piste de la face p (n) est de 500 e- (850e-). Cependant, d'autres mesures réalisées en source pour un module de détection de pré-production ont montré des valeurs plus élevées : 700 et 1100 électrons sur les faces p et n respectivement. Ces valeurs sont prises actuellement comme références pour le simulateur du SSD dans la chaîne de simulation et reconstruction des données de STAR et les performances (simulées) en terme d'efficacité et pureté sont très satisfaisantes [Hip00].
m.
La charge équivalente de bruit pour une piste de la face p (n) est de 500 e- (850e-). Cependant, d'autres mesures réalisées en source pour un module de détection de pré-production ont montré des valeurs plus élevées : 700 et 1100 électrons sur les faces p et n respectivement. Ces valeurs sont prises actuellement comme références pour le simulateur du SSD dans la chaîne de simulation et reconstruction des données de STAR et les performances (simulées) en terme d'efficacité et pureté sont très satisfaisantes [Hip00].
Si les résultats obtenus pour le module de détection révèlent un fonctionnement très satisfaisant des différents éléments, ils valident également les options technologiques, en particulier la connexion par TAB, choisies.
Les modules de détection du SSD font partie d'un programme de R&D commun aux expériences STAR et ALICE. Des doses élevées ont été atteintes (plusieurs dizaines de krad) afin de simuler l'environnement radiatif du LHC. Dans l'expérience STAR, une dose totale de 10 krad pour la couche la plus interne du SVT est considérée réaliste pour les 10 ans de fonctionnement du détecteur [Pan95]. Les modules du SSD, plus éloignés, recevront une dose inférieure : la valeur de 10 krad sera conservée offrant ainsi une marge de sécurité suffisante.
L'irradiation du circuit de lecture était plus problématique. En effet, le circuit est implanté sur un substrat de silicium de 500 ![]() m d'épaisseur et reposait sur un support épais (carte électronique) pour sa fixation et sa connexion. Afin de s'affranchir des phénomènes de diffusion et de perte d'énergie des protons dans cette matière qui auraient perturbé leur comptage, nous avons préféré placer le scintillateur en amont du circuit.
Les doses absorbées étaient évaluées à partir de la relation 3.35 en dose équivalente à celle reçue par le détecteur dans la configuration de la figure 3.40. Ceci permettant une comparaison directe des résultats.
m d'épaisseur et reposait sur un support épais (carte électronique) pour sa fixation et sa connexion. Afin de s'affranchir des phénomènes de diffusion et de perte d'énergie des protons dans cette matière qui auraient perturbé leur comptage, nous avons préféré placer le scintillateur en amont du circuit.
Les doses absorbées étaient évaluées à partir de la relation 3.35 en dose équivalente à celle reçue par le détecteur dans la configuration de la figure 3.40. Ceci permettant une comparaison directe des résultats.
![\begin{figure}
\centering\includegraphics[width=13cm,height=8cm,clip=true,draft=false]
{/home/suire/these/xfigure/Irradiation/piedvsirradCS.eps} \end{figure}](img357.gif) |
Pendant l'irradiation du circuit, une diminution importante des valeurs des piédestaux a été observée, 250 mV initialement à -80 mV en fin d'irradiation (48 kRad3.8). Après 10 krad, la diminution est en moyenne de 35 mV, soit 14%. Le piédestal d'une voie correspond à un niveau continu des étages de préamplification et de mise en forme (cf. section 3.3). Cette variation n'est donc, en soi, pas critique pour le bon fonctionnement du circuit. De plus, il est possible en ajustant les valeurs des paramètres de polarisation du circuit de compenser cette perte et de restaurer aux piédestaux leur valeur initiale []. D'autre part, le bruit moyen des pistes de la face p reste constant de 0 à 30 krad.
Il reste cependant une interrogation sur ces résultats. La diminution d'amplitude des signaux peut également provenir, non pas d'une baisse du gain des chaînes d'amplification, mais du générateur interne lui-même sans que nous puissions trancher. En émettant l'hypothèse d'une perte de gain, nous nous plaçons volontairement dans le cas le plus défavorable. Là encore, il est possible de retrouver le gain initial en modifiant les paramètres de polarisation du circuit.
Nous n'attendions pas de tels événements lors des tests d'irradiation décrits dans cette section, et ce ne fut effectivement pas le cas. L'occurrence de ce phénomène reste entaché de larges incertitudes. Cependant, dans le cadre du SSD de STAR, un système dédié, localisé sur les cartes de connexion (voir figure 2.8) permet, en cas de surconsommation de courant des circuits de lecture, d'éteindre les alimentations qui polarisent le circuit (en réalité, tous les circuits présents sur l'hybride sont éteints). La remise sous tension des circuits suivie du protocole d'initialisation suffit à en rétablir le bon fonctionnement.
Les courants de fuite sur les anneaux de polarisation (I![]() ) et de garde (I
) et de garde (I![]() ) du détecteur ont été mesurés lors de l'irradiation. La figure 3.43 montre leur évolution en fonction de la dose absorbée.
) du détecteur ont été mesurés lors de l'irradiation. La figure 3.43 montre leur évolution en fonction de la dose absorbée.
En premier lieu, nous pouvons remarquer que le bruit sur la face p est plus important que celui de la face n en raison de l'irradiation antérieure du circuit de lecture de la face p. La charge équivalente de bruit, exprimée en électrons, augmente clairement sur les deux faces du détecteur, passant de 890 (670) à 2450 (1790) électrons pour la face p (face n) après 130 krad. Le bruit calculé pour les pistes situées hors du profil de faisceau et par conséquent non-irradiées, reste égal à sa valeur de départ.
Le bruit pour les pistes irradiées est présenté sur la figure 3.44 pour chaque face. L'augmentation du bruit d'une piste (
Il nous est difficile de conclure quant à l'augmentation du bruit pour des doses inférieures à 20 krad. Entre 7 et 17 krad, ![]() b
b![]() est est de l'ordre de 200 électrons pour la face n et 300 pour la face p. Ces valeurs doivent être multipliées par un facteur tenant compte que seule une fraction de la longueur totale des pistes a été irradiée.
est est de l'ordre de 200 électrons pour la face n et 300 pour la face p. Ces valeurs doivent être multipliées par un facteur tenant compte que seule une fraction de la longueur totale des pistes a été irradiée.
Ces tests nous permettent d'affirmer que les modules de détection pour STAR ne subiront pas de pertes significatives de leurs performances initiales à cause de la dose équivalente reçue pendant leur durée de fonctionnement dans l'expérience.
Les circuits de lecture montrent une sensibilité aux particules ionisantes qui se traduit sur les valeurs des piédestaux et des gains. Cependant les effets induits par une dose de 10 krad (équivalente pour le détecteur en silicium) sont aisément compensables. De plus, aucune augmentation de bruit n'a été observée avant 30 krad.
Le détecteur en silicium a également montré un comportement très satisfaisant. La collection des charges n'est pas perturbée même pour de très fortes doses. L'augmentation du bruit est toutefois relativement difficile à quantifier. Si l'on considère des bruits initiaux pour les modules de détection de l'ordre de 700 électrons sur la face p et 1100 électrons sur la face n, alors une dose absorbée de 10 krad conduirait aux valeurs de bruit suivantes : 900 électrons sur la face p et 1120 sur la face n. Soit des rapports signal sur bruit pour une particule au MIP de 28 et 23 sur les faces p et n respectivement. Les deux remarques suivantes permettent cependant d'être optimiste quant à la dégradation du rapport signal sur bruit des modules de détection du SSD :
La réalisation des tests présentés dans ce chapitre nous a permis d'acquérir une connaissance approfondie du fonctionnement des détecteurs en silicium à micropistes et de leur électronique de lecture, le circuit ALICE128C. Ces connaissances ont été mises à profit dans la caractérisation de la méthode de connexion par TAB, qui jusqu'alors n'avait jamais été utilisée dans le domaine des détecteurs en silicium à micropistes. Cette étude a permis de déterminer l'efficacité de connexion. De plus, en révélant certains défauts systématiques, qui ont pu être corrigés, le rendement de la connexion par TAB est supérieur à 99% pour les derniers modules de détection assemblés.
Le module de détection dans sa version finale a été testé sous faisceau au SPS. Les résultats obtenus en terme de résolution en position et de corrélation de charge sont en accord avec les spécifications requises. Ces performances ne seront pas altérées par des dommages dus à l'irradiation pendant la durée de fonctionnement de STAR. Les détecteurs en silicium et le circuit ALICE128C sont parfaitement aptes à supporter une dose de 10 krad qui est nettement supérieure à la dose réelle attendue.
Nous pouvons donc aborder la production du SSD dans son ensemble avec confiance au vu des résultats obtenus pour les modules de détection prototypes. La problématique de la production du SSD sera complètement différente dans la mesure où les tests mis en ![]() uvre pour les premiers modules de détection ne pourront pas être réalisés dans leur ensemble pour chacun des 320 modules de détection qui formeront le SSD.
Nous allons dans le chapitre suivant détailler les tests de production, des détecteurs en silicium et de l'électronique de lecture, préparatoires à la construction du cylindre SSD.
uvre pour les premiers modules de détection ne pourront pas être réalisés dans leur ensemble pour chacun des 320 modules de détection qui formeront le SSD.
Nous allons dans le chapitre suivant détailler les tests de production, des détecteurs en silicium et de l'électronique de lecture, préparatoires à la construction du cylindre SSD.