Maple简介
一、Maple操作界面介绍
1、编辑功能:
编辑功能中查找模块,可以帮助查找你所需要的关键字节.具体操作如图所示:
按上述操作完成后,出现下图所示的对话框:
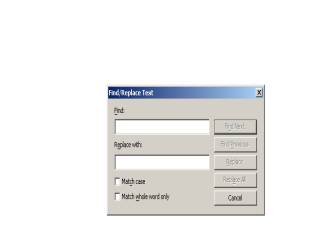
在文本框中输入你要查找的字符或者符号,可以通过findprevious上下翻看,也可以通过replacewith操作替代你所查找的字符或者符号.cancle表示取消操作.
其他编辑操作包括分割或连接(splitorjoin)分为一个执行过程（快截键为f3、f4）和选定块(shift+f3、shift+f4)过程四个操作块
运行操作(Execute)：运行选定或者当前的maple中的语句;
删除运行结果操作（Removeoutput）：将选定或者当前的maple中运行结果从工作爷中删除或者不显示;
2、示图操作（ VIEW）
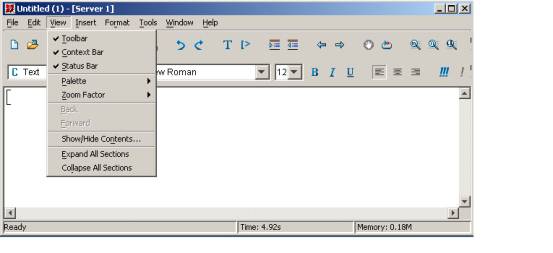
文档在屏幕上的显示模式称为“示图”，maple示图菜单主要设置工作爷文档的一些视图属性，所包括菜单如上图所示。
工具条(toolbar)的功能和其他系统一样，主要包括打开文件、创建新文档、存盘、打印当前页面、复制、剪切、粘贴、撤消操作等。
内容工具条：
“枫叶”表示设置工作页和标准公式和maple语言之间的转换
“X” 表示设置工作页和标准公式在活动和非活动方式之间的转换
“（对号）”表示标准公式有效时自动检查输入表达式的正确性
“！” 表示运行当前表达式
3、插入操作（INSERT）
插入操作比较简单这里就不做详细介绍,主要功能分为:
文本插入(textinput);
标准maple数学表达式插入;
运行单元executegroup插入其中包括在光标前插入和光标后插入
图形插入plot,其中包括两维和三维图象的插入
电子表格插入spreadsheet
段落插入parigraph,其中包括光标前插入和光标后插入
数学输入对象(image)插入
插入超级连接hyperlink
4、其他操作窗口的功能和其他软件基本相同，这里就不做详细介绍了。
二、基本语法规则
MaPle的科学计算功能主要是以命令输入的方式来实现的。Map1e
的命令有自己的使用规则和语法。在使用Maple进行科学计算之前，首先要了解Map1ev命令使用的基本规则。下面给出了利用Maple进行科学计算时的—些基本语法规则
·MapleV的命令在提示符“>”的右边键入，每行命令要以分号“；”结尾。
·命令输入结束按回车键,maple就立即执行该命令
·如果命令以分号结尾，Maple将在下一行给出相应的输出结果，并把光标移到下—个程序段的开始行；如果命令以冒号结尾，Maple
执行命令但不显示输出结果，光标直按移到下一个程序段的开始。
·Maple中乘号为星号“*”，两项相乘时乘号不能省略。
· 对变量赋值时用赋值运算符“：＝”，而不是通常的等号“；”。
· 除号为斜杠符号“／” a 的输入格式为：a/(b+c)。
b+c
·乘方运算符为：“^”或“*’’，负指数必须包含在围括号中。
· 函数的参数必须用圆括号界定，数组或矩阵的下标用方括号界定。
· 变量不需要预先定义，严格区分字母的大小写。
· 在运算符和操作数之间可以插入空格或者其他空白字符，但在运算符和标识符内
部不能插入空格或其他空白字符。
·三个环境变量“%”、“%%”和“%%%”，分别代表当前工作空间最近三次的非空输出结果。
下面给出了Maplev运算的几个例子，内容涉及字符串、数的运算、方程的求解和图像的绘制，可使读者初步认识Map1ev的工作方式。在这些例子中，每行命令都以分号结尾，因此Maple
v在输入的下一行即给出相应的输出，并把光标移到下一个程序段的
开始。
[>“Iam
astring”； “Iamsstring”
[>(3+4)*12;
84
三、maple在数值计算方面的运用
1、整数计算
最基本的，Maple可视为功能强大的
计算器。
计算(32)(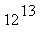
)只需键入：
>32*12^13;
Maple内置大量各类特殊运算如：阶乘；
最大公约数；最小公倍数；模m的同余运算等等。下面是一个阶乘的例子。
>200!;
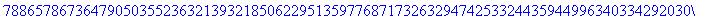
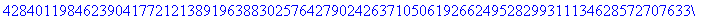
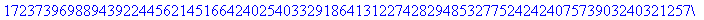
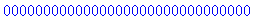
Maple使用百分号%代表对前面输出
的引用。（详情请参考在线帮助）下面的ifactor命令对前面的结果进行因数分解。
>ifactor(%);
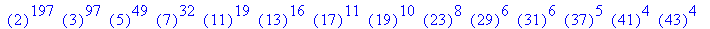
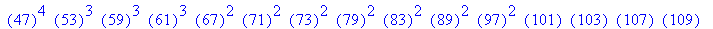
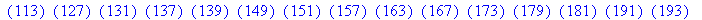
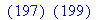
下面的命令又将上式乘开，重新得到200！
>expand(%);
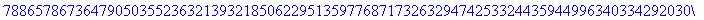
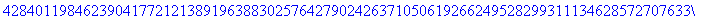
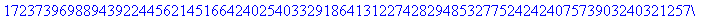
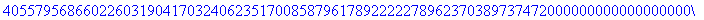
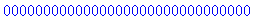
2、浮点运算
Maple的威力首先表现在它的精确运算能
力。无论是分数还是无理数，都不会在运预算过程中自动取近似的十进制小数。这样
避免了误差的叠加。当然如果需要，Maple将给出任意精度的近似小数。
考察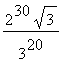
,在Maple中将作如下展开。
>(2^30/3^20)*sqrt(3);
Press[Enter]toseetheresultsof
thisexpression
使用evalf命令,就得到近似的浮点数。
>evalf(%);
3、有限与无限的求和、求积
考察有限和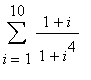
,输入如下。
>Sum((1+i)/(1+i^4),i=1..10);
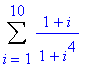
使用value
命令求其值。
>value(%);
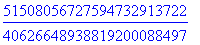
考察无限和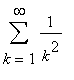
,输入如下。
Ø
Sum(1/k^2,k=1..infinity);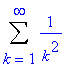
>value(%);
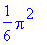
4、复数和特殊函数
Maple一样可以进行复数运算。虚单位使
用大写I
。
Ø
(3+5*I)/(7+4*I);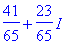
你还可以简单地使用convert函
数将复数的代数形式转化为极坐标表示：(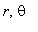
)，r其中是模，
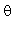是幅
角主值。
>convert(%,polar);
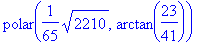
你也可以计算许多初等函数、特殊函数以及数学常数的数值。下例计算自然对数底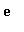
的40位
近似值。
>evalf(exp(1.0),40);
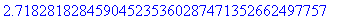
四、maple在代数运算方面的运用
Maple是
一种非常强大的代数运算工具。它可以用符号运算解析的解决和处理许多问题。变量
的定义与使用使得解决“如果……那么”类问题成为可能。
1、展开、分解、化
简表达式
Maple使用不同的方法让数学表达式跟便
于处理、使用。这种变通的特性允许我么进行诸如：多项式展开、因式分解、三角式
化简、用运算结果给变量赋值、恒等变换等操作。
展开、分解表达式
Maple可以展开诸如：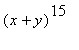
的多
项式。下面的命令创建并展开它。
>expr:=(x+y)^15;
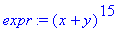
>expand(expr);
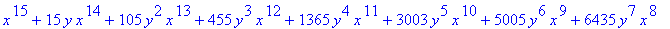
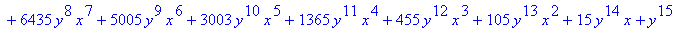
类似的你可以用factor命令对
上面结果进行因式分解来验证。
>factor(%);
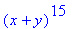
化简表达式
Maple可以使用包括三角恒等式在内的恒
等关系对复杂的表达式进行化简。
考察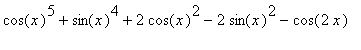
.
>simplify(cos(x)^5+sin(x)^4+2*cos(x)^2-2*sin(x)^2
-cos(2*x));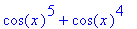
normal
命令是另一种化简的方法，它对分式进行通分和约分。
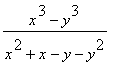化简
>normal((x^3-y^3)/(x^2+x-y-y^2));
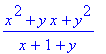
2、表达式变形
命令convert允许你将表达式在各种形式间互化。有效形式
的列表请参阅在线帮助。
下例将分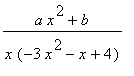式
变为
部分分式。
>my_expr:=(a*x^2+b)/(x*(-3*x^2-x+4));
>convert(my_expr,parfrac,x);
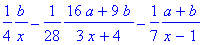
3、解方程（组）
Maple可被用于求解多种代数方程（组）
。
解代数方程
求解如下代数方程：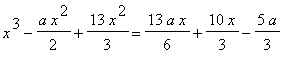
.
>eqn:=x^3-1/2*a*x^2+13/3*x^2=13/6*a*x+10/3*x-5/3*a;
>solve(eqn,{x});
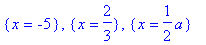
为验根我们计算方程在特殊点x的
值。
>eval(eqn,x=1/2*a);
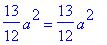
4、解方程组
求解如下5元的方程组：
>eqn1:=a+2*b+3*c+4*d+5*e=41;
>eqn2:=5*a+5*b+4*c+3*d+2*e=20;
>eqn3:=3*b+4*c-8*d+2*e=125;
>eqn4:=a+b+c+d+e=9;
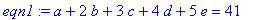
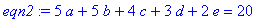
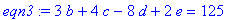
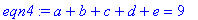
我们可以用变量e来
表示其他未知数a，b，c，d得
到一组解。如果5个未知数一起求，Maple将任选其一作为自由变量
。
>solve({eqn1,eqn2,eqn3,eqn4},{a,b,c,d});
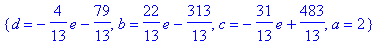
使用所得解验证：eqn1,
eqn2
>eval({eqn1,eqn2},%);
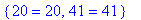
5、解不等式
下例演示在Maple中解不等式如何方
便。
解不等式组：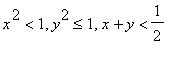
.
>solve({x^2<1,y^2<=1,x+y<1/2},{x,y});
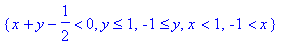
解以y为参量x的不等式：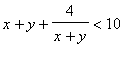
>ineq:=x+y+4/(x+y)<10:
>solve(ineq,{x});
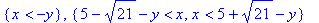
五、maple在绘图方面的运用
Maple支
持2D、3D图象，它可以对显式、隐式、参数型函数及数据集作图。
缺省情况图形将在行内（文档中）显示。
1、图象的动画
plots工具包支持2D、3D动画，用它我们可以描述现实世界中随时间变化
的过程。
>animate3d(cos(t*x)*sin(t*y),x=-Pi..Pi,y=-Pi..Pi,
t=1..2);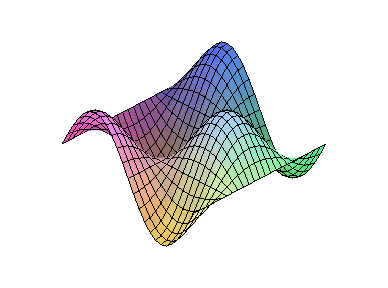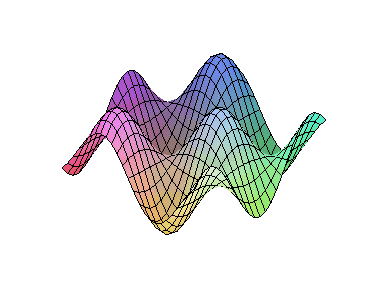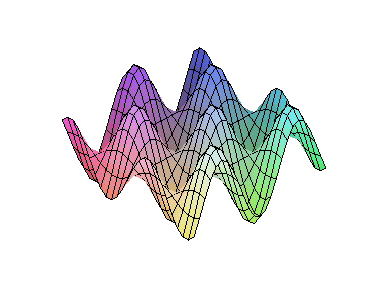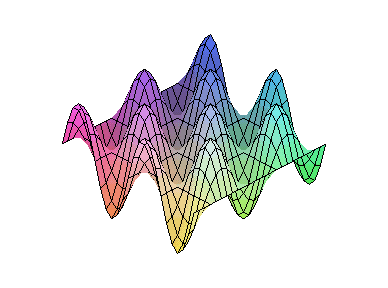
2、线性不等数组的
图解
Maple能对线性不等式组作图，使许多线
性规划问题的解可视化。
Maple命令inequal将
对以下不等式组作图：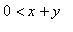
,
,
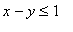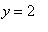
>inequal({x+y>0,x-y<=1,y=2},x=-3..3,
y=-3..3,
optionsfeasible=(color=red),optionsopen=(color=blue,
thickness=2),optionsclosed=(color=green,thickness=3),
optionsexcluded=(color=yellow));
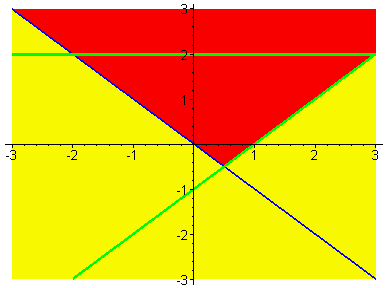
3、2D图象
Maple的2D作图工具允许同时对多函数作
图，生成复函数映射、对数、双对数、参数型、分段、极坐标、等值线等图象。我们
还可以对不等式组、隐函数、微分方程的解、根的分布等作图。另外题目、标签、文
字的字体属性亦可随心所欲。
2D作图举例
下例生成
的图
像。
>plot(tan(x),x=-2*Pi..2*Pi,y=-4..4,discont=true,
title=`y=tan(x)`);
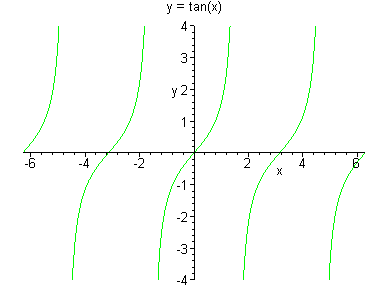
请留意Maple如何处理函数的不连续
点。
4、implicitplot（隐函数作图）
命令
plots工具包中的命令：implicitplot生成由二元方
程决定的隐函数图象。
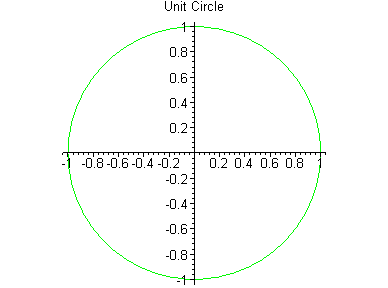
下例同时生成单位圆：
和指数函数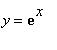
的图象:
>implicitplot({x^2+y^2=1,y=exp(x)},x=-Pi..Pi,
y=-Pi..Pi,
scaling=CONSTRAINED);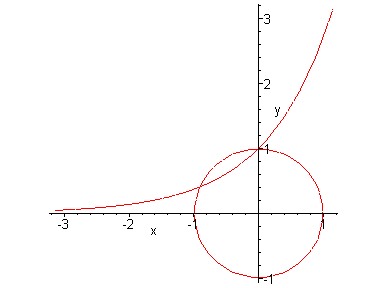
plottools
工具包含有许多生成和处理图形对象的命令，如单位圆:
>c:=circle([0,0],1,color=green):
>display(c,scaling=CONSTRAINED,title=`UnitCircle`
);
5、3D图象
Maple可以生成由显函数、参数型、微分
方程的解给出的3D曲线和曲面。图像的外观如：字体、光照、着色等也可随便更改。
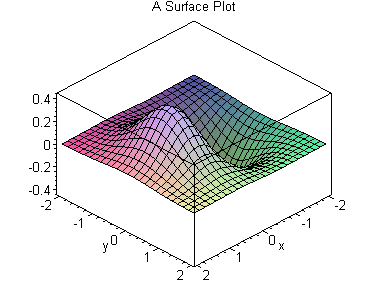
下例将生成二元函数：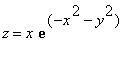
的图
象。
>plot3d(x*exp(-x^2-y^2),x=-2..2,y=-2..2,axes=BOXED,
title=`ASurfacePlot`);
六、maple在微积分方面的运用
Maple提
供多种强力工具用以解决一元或多元微积分问题。Maple可被用于求解微分、积分、极
限、级数展开、级数求和、求、积分变换（如拉普拉斯变换、Z变换、梅林变换、傅利
叶变换等）、以及分段函数等诸多领域的问题。Maple不仅能够给出以上问题的数值解
，他强大的引擎同样提供解析解（符号解）。
1、微积分
Maple能给出微分与积分结果的符号表达
。例如：定义函数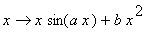
.
>f:=x->x*sin(a*x)+b*x^2;
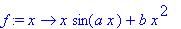
对x取偏微，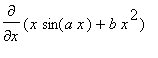
,将结果存于变量
.
>Diff(f(x),x);
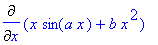
>f_prime:=value(%);
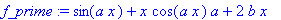
如求
的原
函数就应得到f(x)。验证如
下，计算：
>Int(f_prime,x);
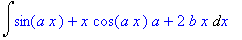
>value(%);
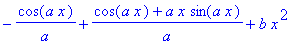
>simplify(%);
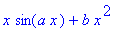
2、定积分
Maple可用于计算定积分，例如将上例积分
取区间：x=1到x=2的定积分：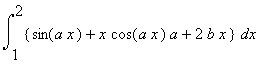
.
>Int(f_prime,x=1..2);
>value(%);
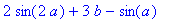
3、极限
Maple能计算趋向有限值获趋向无穷的极
限，能求左右极限以及含有绝对值符号的极限问题。不收敛的情况Maple也可辨识。
求极限
例如：
>expr:=(2*x+3)/(7*x+5);
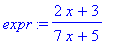
>Limit(expr,x=infinity);
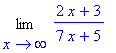
>value(%);
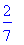
七、maple在线形代数方面的运用
Maple中最常用的工具包就是线性
代数工具包：linalg.该工具包提供了一组用于处理向量、矩阵的强力工具。Maple求矩阵标准型，能求特征值、特征向量，定义曲线坐
标，进行各种矩阵分解如：Cholesky,LU,和QR分解。
1、行列式求值与求逆矩阵
定义3X3矩阵A如下：
>A:=matrix(3,3,
[1/2,-1/3,2,-5,14/3,9,0,11,-5/6]);
使用det命令计算其行列式值
。
>det(A);
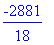
由于行列式不为0（可逆），于是我
们使用inverse命令求其逆矩阵。
Ø
inverse(A);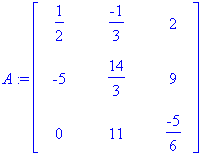
使用det命令计算其行列式值
。
>det(A);
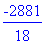
由于行列式不为0（可逆），于是我
们使用inverse命令求其逆矩阵。
>inverse(A);
定义另一矩阵B,含有变量：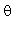
，
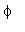
>B:=matrix(3,3,[1/2,0,-2,sin(theta),1,phi^2,
0,
phi-1,3/4]);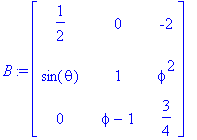
求矩阵A、B的积并存于C.
C:=multiply(A,B);
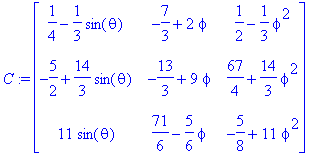
再求行列式。
>det(C);
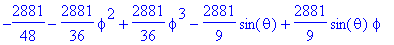
2、特征值与特征向量
使用eigenvects命令可求矩阵的特征向量。返回结果列表中的第一分量是特征值，
第二分量是它的代数重数，最后一个分量是该特征值对应的特征空间的基向量组成的
集合。
>M:=matrix(3,3,[1,-3,3,3,-5,3,6,-6,4]
);
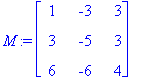
>eigenvects(M);
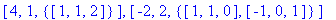
3、特殊矩阵
linalg工具包含有大多数数学中出现的特殊矩阵，如Hilbert,
Vandermonde,Frobenius等矩阵。
例如生成6X6Hilbert矩阵。
>hilbert(6);
Maple亦可生成变量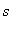
,
,
,
,
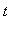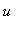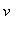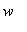的范德蒙（Vandermonde）矩阵.
>vandermonde([s,t,u,v,w]);
