Next: ITR Contribution and Stability Up: Inclusive Production Cross Sections Previous: Luminosity Determination Contents
In order to understand differences between MC and data, a comparison of
the main kinematical variables is performed.
For each bin an invariant mass distribution for the corresponding ![]() candidate
is produced. All obtained distributions are fitted by a Gaussian plus a polynominal
of second order to describe the background. Finally in order to simplify the comparison, distributions of
kinematical variables for data and MC are normalized to the same area.
candidate
is produced. All obtained distributions are fitted by a Gaussian plus a polynominal
of second order to describe the background. Finally in order to simplify the comparison, distributions of
kinematical variables for data and MC are normalized to the same area.
The following kinematical variables are compared:
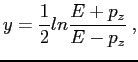 |
(6.17) |
| (6.18) |
The distributions of ![]() and
and ![]() are of special interest for this analysis.
In case of
are of special interest for this analysis.
In case of ![]() MC and data show an agreement on the level of 10-20%.
The simulated distribution of
MC and data show an agreement on the level of 10-20%.
The simulated distribution of ![]() for
for ![]() is within 25% in agreement with data,
is within 25% in agreement with data, ![]() distribution within 30%.
The
distribution within 30%.
The ![]() distribution of
distribution of
![]() demonstrated a better agreement, the maximum reached difference is o f the order of 15%, in case of
demonstrated a better agreement, the maximum reached difference is o f the order of 15%, in case of ![]() distribution it is 30%.
distribution it is 30%.
Above a ![]() of about 0.8
of about 0.8 ![]() the distributions for all three particles show
large differences between MC and data.
Such behaviour is due to a simplified model used in MC,
the distributions for all three particles show
large differences between MC and data.
Such behaviour is due to a simplified model used in MC, ![]() spectra is simulated
with one exponential. Data distributions indicate that it is
better described by two exponentials. This behavior is well known and
was mentioned already by [#!Mple!#].
spectra is simulated
with one exponential. Data distributions indicate that it is
better described by two exponentials. This behavior is well known and
was mentioned already by [#!Mple!#].