



Next: Les conclusions
Up: Résultats
Previous: Evaluation du module de
Pour évaluer la qualité de l'association des clusters face à face, nous allons procéder ainsi: les points d'impact reconstruits sont classés en trois catégories : les bons, les points d'impact perdus qui correspondent à au moins un cluster perdu sur l'une des faces et les points d'impact de bruit où au moins l'un des clusters est un cluster de bruit. Parmi tous les points issus de différentes configurations, nous n'évaluons que les points ayant une probabilité d'existence supérieure à 50%. En réalité, cette sélection devra être effectuée par le programme de trajectographie qui associe les points aux traces en fonction de la qualité du point. Les différents points d'impact sont également classés par rapport à la configuration dont ils proviennent (1-1, 2-1, 2-2, ... qui correspond au nombre de clusters sur chacune des faces) comme indiqué sur dans le tableau 3.3.3.
Tableau 3.3:
Efficacité et pureté des points d'impact obtenus par le module d'association
| |
Qualité de détecteur parfaite |
| |
Pistes mortes 0% |
| |
Pistes bruyantes 0% |
| |
bon |
bruit |
perdu |
efficacité |
pureté |
| config. 1-1 |
17710 |
0 |
207 |
98.84 % |
100.00 % |
| config. 1-2 |
823 |
45 |
27 |
96.82 % |
84.82 % |
| config. 2-2 |
2285 |
91 |
62 |
97.36 % |
96.17 % |
| config. 2-3 |
159 |
13 |
31 |
83.68 % |
92.44 % |
| config. 3-3 |
226 |
26 |
56 |
80.14 % |
89.68 % |
| Total |
21203 |
175 |
383 |
98.92 % |
99.18 % |
| |
| |
Qualité de détecteur réaliste |
| |
Pistes mortes 3% |
| |
Pistes bruyantes 4% |
| |
bon |
bruit |
perdu |
efficacité |
pureté |
| config. 1-1 |
16812 |
0 |
197 |
98.84 % |
100.00 % |
| config. 1-2 |
964 |
108 |
34 |
96.59 % |
89.93 % |
| config. 2-2 |
2024 |
112 |
73 |
96.52 % |
94.76 % |
| config. 2-3 |
160 |
34 |
31 |
83.77 % |
82.47 % |
| config. 3-3 |
185 |
29 |
49 |
79.06 % |
86.45 % |
| Total |
20146 |
283 |
384 |
96.16 % |
98.61 % |
|
Comme précédement, l'efficacité est égale au rapport
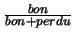 sauf pour le total où le dénominateur est le nombre de points d'impact localisés dans la zone active du détecteur. Par conséquent, l'efficacité totale mesure la qualité de la reconstruction dans son ensemble (SCF + SCM). Quant à la pureté, elle est toujours égale à
sauf pour le total où le dénominateur est le nombre de points d'impact localisés dans la zone active du détecteur. Par conséquent, l'efficacité totale mesure la qualité de la reconstruction dans son ensemble (SCF + SCM). Quant à la pureté, elle est toujours égale à
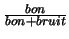 dans les deux cas. On notera que bon+perdu (21585) pour le total des configurations dans le cas de détecteurs parfaits est légèrement inférieur au nombre de points présents dans la région active du détecteur (21692). Ceci provient de la coupure en probabilité d'existence fixée à 50 % pouvant rejeter des bons points d'impact qui, en raison d'une mauvaise reconstruction (due à la séparation de clusters recouverts) ou à la résolution en charge collectée n'ont pas une bonne pondération.
Les configurations 1-1 et 2-1 correspondent à des cas non ambigus où une solution unique par association géométrique est toujours possible. Ces deux configurations représentent environ 87% des bons points d'impact reconstruits. Si la technique d'association par comparaison de charge n'était pas utilisée, nous aurions une efficacité globale de 85 % à comparer avec les 98.9 % en utilisant la méthode de comparaison des charges. On notera également que la pureté globale après association des clusters est supérieure à celle que nous avions trouvée pour les clusters. Comme espéré, ceci est dû à la réjection des clusters de bruit lors de la phase d'association.
dans les deux cas. On notera que bon+perdu (21585) pour le total des configurations dans le cas de détecteurs parfaits est légèrement inférieur au nombre de points présents dans la région active du détecteur (21692). Ceci provient de la coupure en probabilité d'existence fixée à 50 % pouvant rejeter des bons points d'impact qui, en raison d'une mauvaise reconstruction (due à la séparation de clusters recouverts) ou à la résolution en charge collectée n'ont pas une bonne pondération.
Les configurations 1-1 et 2-1 correspondent à des cas non ambigus où une solution unique par association géométrique est toujours possible. Ces deux configurations représentent environ 87% des bons points d'impact reconstruits. Si la technique d'association par comparaison de charge n'était pas utilisée, nous aurions une efficacité globale de 85 % à comparer avec les 98.9 % en utilisant la méthode de comparaison des charges. On notera également que la pureté globale après association des clusters est supérieure à celle que nous avions trouvée pour les clusters. Comme espéré, ceci est dû à la réjection des clusters de bruit lors de la phase d'association.
Concernant la résolution en position des points d'impact reconstruits, il est intéressant de la définir dans le repère de STAR suivant  (l'axe du faisceau) et suivant
(l'axe du faisceau) et suivant 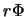 (la direction transverse) puisque ces résolutions projetées seront directement utilisées pour la reconstruction des trajectoires. La figure 3.19 décrit les deux repères utilisés pour localiser les points d'impact: l'un dans le système de coordonnées des pistes (
(la direction transverse) puisque ces résolutions projetées seront directement utilisées pour la reconstruction des trajectoires. La figure 3.19 décrit les deux repères utilisés pour localiser les points d'impact: l'un dans le système de coordonnées des pistes (
 ), l'autre dans le référentiel global de STAR (
), l'autre dans le référentiel global de STAR (
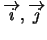 ) avec
) avec
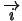 suivant la direction
suivant la direction 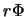 et
et
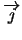 suivant Z.
suivant Z.
Figure 3.19:
Changement du repère (u,v) au repère (i,j).
|
|
Nous avons alors les relations suivantes:
et
or
et
avec
ce qui mène à:
En passant aux résolutions et en supposant que
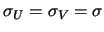 ce qui est raisonnable, nous obtenons :
ce qui est raisonnable, nous obtenons :
En prenant
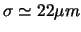 , comme nous l'avions calculé dans la partie 2.2, nous obtenons les estimations de la résolution dans le repère global de STAR suivantes:
, comme nous l'avions calculé dans la partie 2.2, nous obtenons les estimations de la résolution dans le repère global de STAR suivantes:
Ces prédictions sont tout à fait en accord avec les résolutions issues des simulations comme le montre la figure 3.20
Figure 3.20:
Résolutions suivant les directions 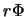 et
et  du SSD.
du SSD.
|
|




Next: Les conclusions
Up: Résultats
Previous: Evaluation du module de
Walter Pinganaud 11 Octobre 2000
![]() (l'axe du faisceau) et suivant
(l'axe du faisceau) et suivant ![]() (la direction transverse) puisque ces résolutions projetées seront directement utilisées pour la reconstruction des trajectoires. La figure 3.19 décrit les deux repères utilisés pour localiser les points d'impact: l'un dans le système de coordonnées des pistes (
(la direction transverse) puisque ces résolutions projetées seront directement utilisées pour la reconstruction des trajectoires. La figure 3.19 décrit les deux repères utilisés pour localiser les points d'impact: l'un dans le système de coordonnées des pistes (
![]() ), l'autre dans le référentiel global de STAR (
), l'autre dans le référentiel global de STAR (
![]() ) avec
) avec
![]() suivant la direction
suivant la direction ![]() et
et
![]() suivant Z.
suivant Z.