



Next: The double differential multiplicity
Up: Cross-talk analysis
Previous: Cross-talk evaluation: results and
Contents
Kopytine's homepage
Cross-talk correction for the multiplicity
It is clear that the cross-talk between neighbouring channels not
only influences the correlation/fluctuation content of the observed
events, but, being effectively positive, makes the measured multiplicity
systematically larger.
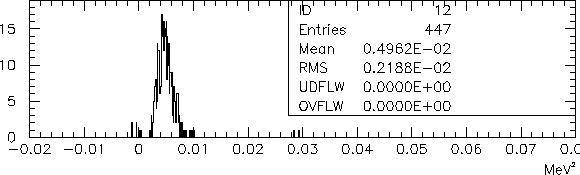
Figure 6.9:
A distribution of the covariance matrix elements, that represent
correlations between adjacent inner channels of sectors.
Matrix elements involving dead channels are not shown.
Run 3192.
 |
In this section I convert the knowledge of the 9% cross-talk effect
(subsection 6.5.4)
into a down-scaling correction factor for the total
multiplicity.
The simplest way of doing it is to say that
a fitted multiplicity, based on weights 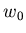 ,
, 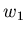 ,
, 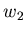 ...
(see formula 3.2), can be approximated by
taking the total energy deposited in a pad over the run and dividing
it by mean energy
...
(see formula 3.2), can be approximated by
taking the total energy deposited in a pad over the run and dividing
it by mean energy
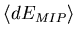 .
This is equivalent to saying that multiplicity
is, effectively, proportional to the amplitude.
Then, the extra
multiplicity induced by the cross-talk from a typical adjacent channel
is, on the average, a 9% addition, and this number needs to be
multiplied by 2 for a typical channel which has two neighbours.
More accurately, 14 out of 16 channels have two neighbours and 2 have
1 neighbour, therefore on the average the factor is
.
This is equivalent to saying that multiplicity
is, effectively, proportional to the amplitude.
Then, the extra
multiplicity induced by the cross-talk from a typical adjacent channel
is, on the average, a 9% addition, and this number needs to be
multiplied by 2 for a typical channel which has two neighbours.
More accurately, 14 out of 16 channels have two neighbours and 2 have
1 neighbour, therefore on the average the factor is
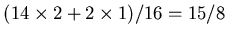 rather than 2.
The best is to take the subsample of the channel pairs from
Fig. 6.7 such that both channels are inner channels,
and use Eq. 6.33 to get the effective coupling
rather than 2.
The best is to take the subsample of the channel pairs from
Fig. 6.7 such that both channels are inner channels,
and use Eq. 6.33 to get the effective coupling 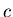 .
Then the multiplicity correction factor becomes
.
Then the multiplicity correction factor becomes
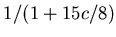 .
The distribution of the covariance matrix elements for such pairs
is shown in Fig. 6.9.
With its input, the correction factor becomes 0.86.
A necessary caveat is that the 9% cross-talk is merely an ``effective'',
approximate and integral way of looking at the problem.
The level of approximateness implied by using the single correction for all
channels is therefore not a reduction of accuracy, as compared to what
has been done in Subsection 6.5.4.
.
The distribution of the covariance matrix elements for such pairs
is shown in Fig. 6.9.
With its input, the correction factor becomes 0.86.
A necessary caveat is that the 9% cross-talk is merely an ``effective'',
approximate and integral way of looking at the problem.
The level of approximateness implied by using the single correction for all
channels is therefore not a reduction of accuracy, as compared to what
has been done in Subsection 6.5.4.




Next: The double differential multiplicity
Up: Cross-talk analysis
Previous: Cross-talk evaluation: results and
Contents
Mikhail Kopytine
2001-08-09

